AcWing 107. 超快速排序

超快速排序

一、引理：逆序数

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。

排列的逆序数等于该排列转化为自然排序（从小到大）的最小次数
例如：\(31425\) 的逆序数为\(3\)

• \(3\)无逆序，则\(n_1 = 0\)，

• \(1\)逆序有\(3\)，则\(n_2 = 1\)，

• \(4\)无逆序，则\(n_3 = 0\)，

• \(2\)逆序有\(3,4\)，则\(n_4 = 2\)，

• \(5\)无逆序，则\(n_5 = 0\)，

若将该序列转化成从小到大排序，需要\(\large (n_1 + n_2 + n_3 + n_4 + n_5)=3\)次交换。

二、直接计算

计算一个排列的逆序数的直接方法是逐个枚举逆序，同时统计个数。例如在序列 \(\{3, 1, 4, 2, 5 \}\) 中，逆序依次为 \((3,1)，(3,2)，(4,3)\)，因此该序列的逆序数为 \(3\)。

三、归并排序

直接计数法虽然简单直观，但是其时间复杂度是\(O(n^2)\)。一个更快的计算方法是在归并排序的同时计算逆序数。且该方法只是交换相邻的两个元素，符合题意。

四、算法分析

归并排序

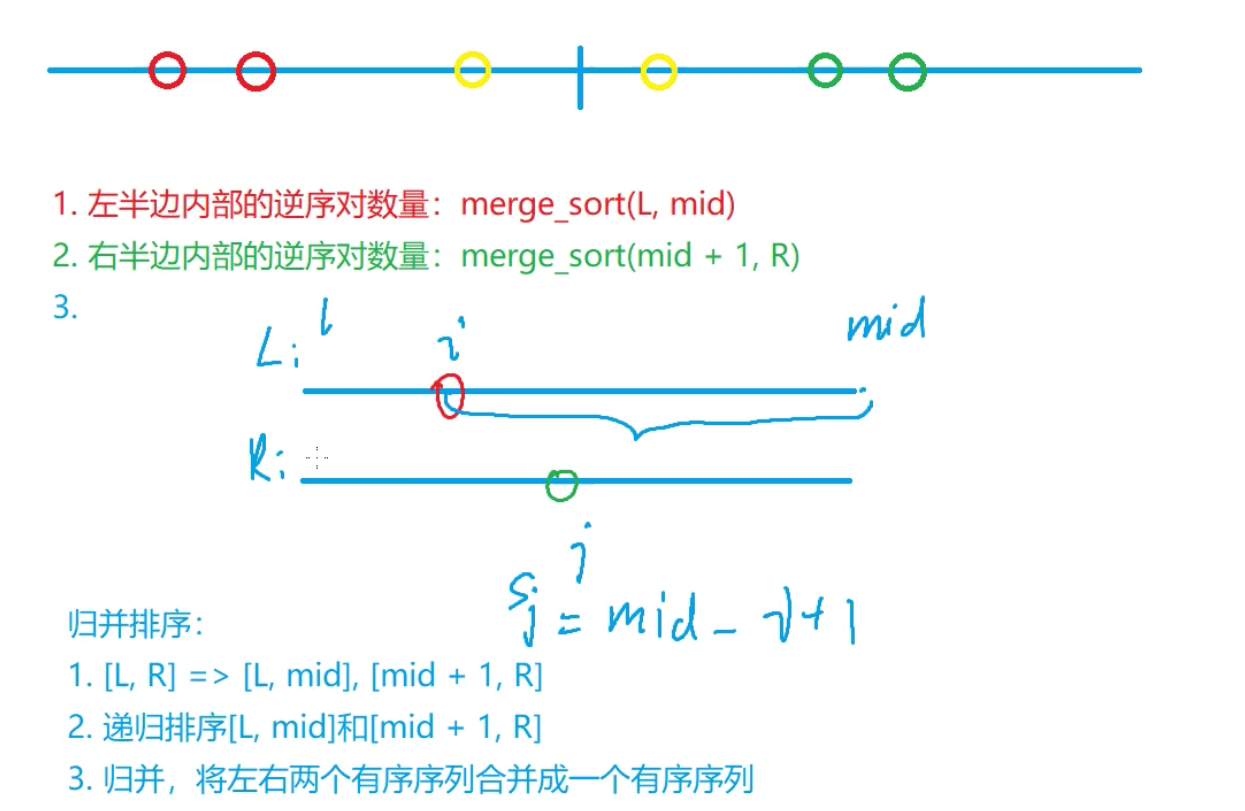
• 给定两个有序序列，从右边序列中最小的元素开始往左边序列中插入，设右边序列中选定的元素的位置为j，左边序列选定的元素位置为i，中间位置为mid，则此时交换的位置次数是(mid - i + 1)，最后把所有归并后交换的次数累加在一起即可。

• 例如 \(31425\) 经过归并后得出两个有序序列 \(134\) 和 \(25\) （注意：\(314\)也是需要归并交换位置得到\(123\)的）即将\(2\)插入到\(3\)位置前，此操作相当于交换了两次位置，设\(3\)元素的位置为\(i\)，\(4\)元素的位置是中间位置\(mid\)，则此时交换的次数为\((mid - i + 1) = 2\)次

附上主播的图

五、实现代码

#include <bits/stdc++.h>
typedef long long LL;
const int N = 500010;
int n;
LL q[N], tmp[N];

LL merge_sort(int l, int r) {
    if (l >= r) return 0;
    int mid = (l + r) >> 1;

    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);

    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else {
            res += mid - i + 1; //如果q[i]>q[j],那么 i~mid之间所有数字，都>q[j]
            tmp[k++] = q[j++];
        }
    //清理剩余
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    //抄回来
    for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
    return res;
}

int main() {
    while (scanf("%d", &n), n) {
        for (int i = 0; i < n; i++) scanf("%d", &q[i]);
        printf("%lld\n", merge_sort(0, n - 1));
    }
    return 0;
}

标签：int,序数,mid,AcWing,序列,排序,107,逆序
来源： https://www.cnblogs.com/littlehb/p/16441707.html