问题描述

给你一个 m x n 的整数网格图 grid ，你可以从一个格子移动到 4 个方向相邻的任意一个格子。

请你返回在网格图中从 任意 格子出发，达到 任意 格子，且路径中的数字是 严格递增 的路径数目。由于答案可能会很大，请将结果对 109 + 7 取余 后返回。

如果两条路径中访问过的格子不是完全相同的，那么它们视为两条不同的路径。

示例 1：

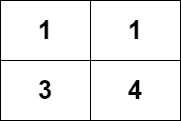
输入：grid = [[1,1],[3,4]]
输出：8
解释：严格递增路径包括：

• 长度为 1 的路径：[1]，[1]，[3]，[4] 。
• 长度为 2 的路径：[1 -> 3]，[1 -> 4]，[3 -> 4] 。
• 长度为 3 的路径：[1 -> 3 -> 4] 。
  路径数目为 4 + 3 + 1 = 8 。
  示例 2：

输入：grid = [[1],[2]]
输出：3
解释：严格递增路径包括：

• 长度为 1 的路径：[1]，[2] 。
• 长度为 2 的路径：[1 -> 2] 。
  路径数目为 2 + 1 = 3 。

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 1000
1 <= m * n <= 105
1 <= grid[i][j] <= 105

问题求解

dp[i][j]为以i，j为起点的递增数目，记忆化搜索即可。

class Solution:
    def countPaths(self, grid: List[List[int]]) -> int:
        mod = 10 ** 9 + 7
        m, n = len(grid), len(grid[0])
        res = 0
        
        @cache
        def dfs(i, j):
            res = 1
            for ni, nj in (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1):
                if 0 <= ni < m and 0 <= nj < n and grid[ni][nj] > grid[i][j]:
                    res = (res + dfs(ni, nj)) % mod
            return res
        
        for i in range(m):
            for j in range(n):
                res = (res + dfs(i, j)) % mod
        
        return res

标签：格子,res,递增,路径,6110,网格,grid,长度
来源： https://www.cnblogs.com/hyserendipity/p/16441319.html