AcWing 105 七夕祭

题目传送门

一、核心问题分析

我的解法涉及一个贪心模板 ，请先看透这个题 :糖果传递

首先提醒一下，在一行中，各列摊位之间交换位置，是不改变行的摊位数量的。列同理。
我们模拟一下交换的过程：

假设七夕祭有\(12\)个摊位，图中有红圈的是题目主角喜欢的摊位。

​ 经过两轮交换后各列的摊位的红圈的数量都一样了，但各行的红圈数量没有发生过变化。

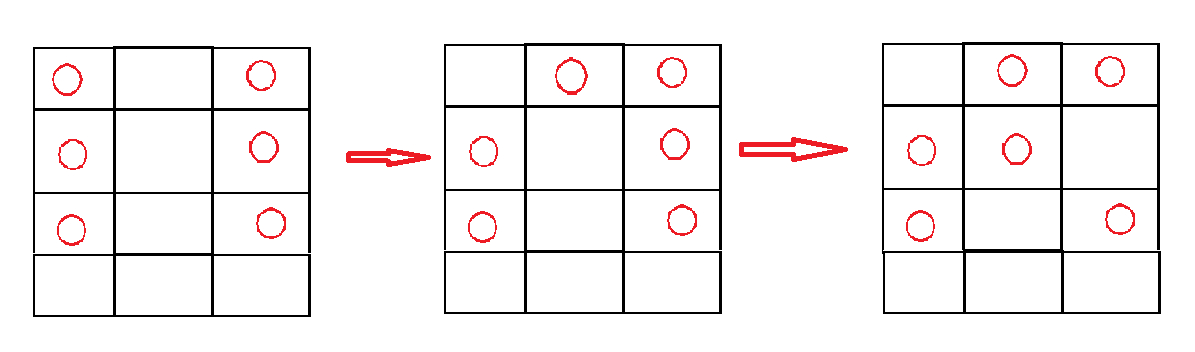
这个题和 糖果传递 那个题有什么关联呢？

别急，我先把这个图改一改（把线擦去了）。

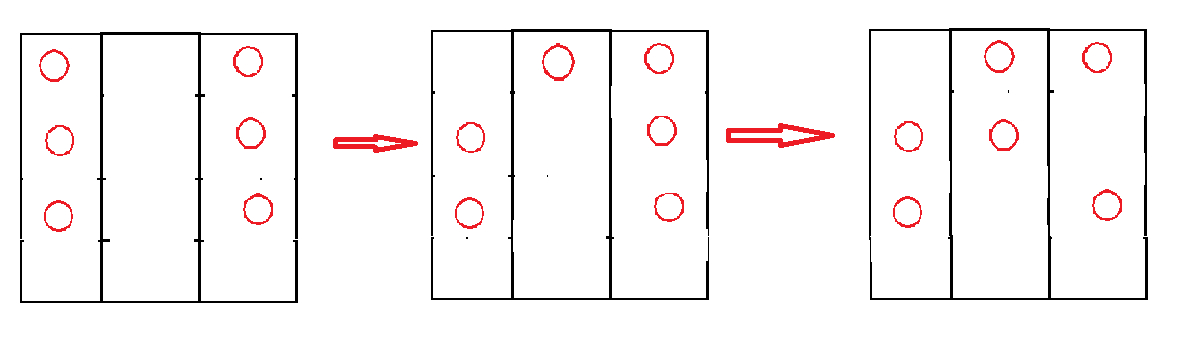
你们看，这些红圈像不像糖果，哈哈哈哈哈哈哈哈，相邻列之间交换摊位，就像是相邻两个小朋友正交换糖果嘛。

算法思路：
因为行之间的交换苹果，并不影响列；列之间交换苹果，并不影响行，现在我们想求的是

\[\large min(行变更次数+列变更次数) \]

而行变更与列变更是个自独立的，我们就可以先计算行变更最小值，再计算列变更最小值，加在一起就是答案。

二、实现代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 100010;

int row[N], col[N], s[N], c[N];

LL work(int n, int a[]) {
    //前缀和
    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
    //不能整除，最终无法完成平均工作
    if (s[n] % n) return -1;
    //平均数
    int avg = s[n] / n;
    //构建c数组
    c[1] = 0;
    for (int i = 2; i <= n; i++) c[i] = s[i - 1] - (i - 1) * avg;
    //排序，为求中位数做准备
    sort(c + 1, c + n + 1);

    //计算每个c[i]与中位数的差,注意下标从1开始时的写法 c[(n+1)/2]
    LL res = 0;
    for (int i = 1; i <= n; i++) res += abs(c[i] - c[(n + 1) / 2]);

    return res;
}

int main() {
    int n, m, T;
    scanf("%d%d%d", &n, &m, &T);

    while (T--) {
        int x, y;
        scanf("%d%d", &x, &y);
        row[x]++, col[y]++;
    }

    LL r = work(n, row);
    LL c = work(m, col);

    if (r != -1 && c != -1)
        printf("both %lld\n", r + c);
    else if (r != -1)
        printf("row %lld\n", r);
    else if (c != -1)
        printf("column %lld\n", c);
    else
        printf("impossible\n");

    return 0;
}

标签：int,交换,红圈,摊位,变更,105,糖果,七夕,AcWing
来源： https://www.cnblogs.com/littlehb/p/16438197.html