首页 > 其他分享> > dp 好题

dp 好题

2022-07-01 22:33:34 作者：互联网

AGC002F Leftmost Ball

给你 \(n\) 种颜色的球，每个球有 \(k\) 个，把这 \(n\times k\) 个球排成一排，把每一种颜色的最左边出现的球涂成白色(初始球不包含白色)，求有多少种不同的颜色序列，答案对 \(10^9+7\) 取模。

将这 \(n\times k\) 个球看成 \(n\) 个白球和 \(n\times k - n\) 个其他颜色的球，由于白球是每种颜色的第一个，所以要保证对于每个位置前缀白球个数均大于等于其他颜色种类数。

设 \(f_{i,j}\) 表示已经放了 \(i\) 个白球和 \(j\) 个其他球的方案数 \((i\ge j)\)。

转移时考虑最后一个放的什么：

白球：\(f_{i-1,j}\)
新的颜色：\(f_{i,j-1}\times (n-j+1) \times \binom{n\times k-i-(j-1)\times(k-1)-1}{k-2}\)

这里，我们将每个颜色的球的贡献全算上，在剩下 \(n-j+1\) 个颜色中任选一个放在 \(i\)，然后该颜色还剩 \(k-2\) 个球，放在后面 \(n\times k-i-(j-1)\times(k-1)-1\) 个空中。

AGC001E BBQ Hard

有 \(n\) 个数对 \((a_i,b_i)\)，求出

\[\sum_{i=1}^{n}\sum_{j=i + 1}^{n}{a_i+b_i+a_j+b_j \choose a_i+a_j} \]
答案对 \(10^9+7\) 取模

\(2\le n \le 200000,1\le a_i,b_i\le 2000\)

观察到 \(n\) 很大而值域很小，考虑对值域进行操作。

\(\binom{a_i+b_i+a_j+b_j}{a_i+a_j}\) 这个形式其实就是在坐标系上从 \((-a_i,-b_i)\) 只能向上或向右走，走到 \((a_j,b_j)\) 的方案数，所以我们就是要求任意两点间路径方案数的和。

考虑如何把复杂度降下来，如果能对每个点算其他所有点到它的路径方案数，就可以 \(O(n)\) 枚举了。

设 \(f_{i,j}\) 表示所有关键点到 \((i,j)\) 的方案数之和，转移也很简单 \(f_{i,j} = f_{i-1,j}+f_{i,j-1}\)，初值 \(f_{-a_i,-b_i}=1\)。

但题目要求 \(i<j\)，所以减掉 \(\binom{a_i+b_i+a_i+b_i}{a_i+a_i}\) 后除以 \(2\) 即可。

ARC074C RGB Sequence

有一个序列 \(\left\{a_{i}\right\}\)，要给序列中的每个元素一种颜色：红/绿/蓝。有 \(M\) 条限制 \((l,r,x)\)，表示格子 \([l,r]\) 中颜色的种数要恰好为 \(x\)，问可行的方案数，答案对 \(10^9+7\) 取模。

\(1\le n,m\le 3000\)

观察到只有三种颜色，所以可以记录下每个颜色最后出现的位置。

设 \(f_{i,j,k}\) 表示考虑到第 \(i\) 个数，另外两种颜色最后出现在 \(j\) 和 \(k\)，钦定 \(j>k\)，转移很显然

\(f_{i+1,j,k}+=f_{i,j,k}\)
\(f_{i+1,i,k}+=f_{i,j,k}\)
\(f_{i+1,i,j}+=f_{i,j,k}\)

对于限制，挂到 \(r\) 上，在每次向后转移前更新一遍，由于已经知道了另外两个颜色最后的位置，就可以得到 \([l,r]\) 中的颜色数了，将不合法的改为 \(0\) 即可。

P2501 [HAOI2006]数字序列

给定一个长度为 \(n\) 的序列 a，求最少需要改变多少个数才能让 \(a\) 单调严格上升，同时每个数改变的绝对值之和最小是多少。

\(1\le n\le 3.5\times 10^4,1\le a_i\le 10^5\)

第一问

考虑保留最多的数，对于 \(i<j\)，如果 \(a_i,a_j\) 可以保留，那么至少 \(a_j-a_i\ge j-i\)，也就是 \(a_i-i\le a_j-j\)。

设 \(b_i=a_i-i\)，其最长不下降子序列即为答案。

第二问

在第一问的基础上，找到两个在 \(b\) 的最长不下降子序列上相邻的点 \(i,j\)，那么 \(\forall k \in (i,j),b_k<a_i 或 b_k>b_j\)，我们要把中间的这部分改成合法的，不难想到最优情况下一定是前一部分改成 \(b_i\)，后一部分改成 \(b_j\)，这个中间点直接枚举是可以过的（

同时 dp 记录一下 \(f_i\) 表示 \([1,i]\) 都合法的最小代价即可。

P3943 星空

有一串长为 \(n\) 的灯泡，其中有 \(k\) 个灯是关的。给定 \(m\) 个可以翻转的长度，也就是每次可以翻转这 \(m\) 个长度之一的灯泡，求最少操作多少次可以将所有灯泡打开。

\(n \le 40000, m\le 64,k\le 8\)

将灯的开关状态看为 \(0/1\)，每次操作都是让一段区间异或 \(1\)。这种区间操作可以利用差分，这样每次操作修改两个位置。

由于最多有 \(8\) 个灯是关着的，所以差分数组中最多有 \(16\) 个 \(1\)，我们要把这些 \(1\) 都改成 \(0\)，预处理出相邻两个之间的距离状压 dp 即可。

具体来说，先 bfs 求出想改变两个相距 \(x\) 的位置的状态最少需要操作几次，然后转移时枚举最后修改的两个位置。

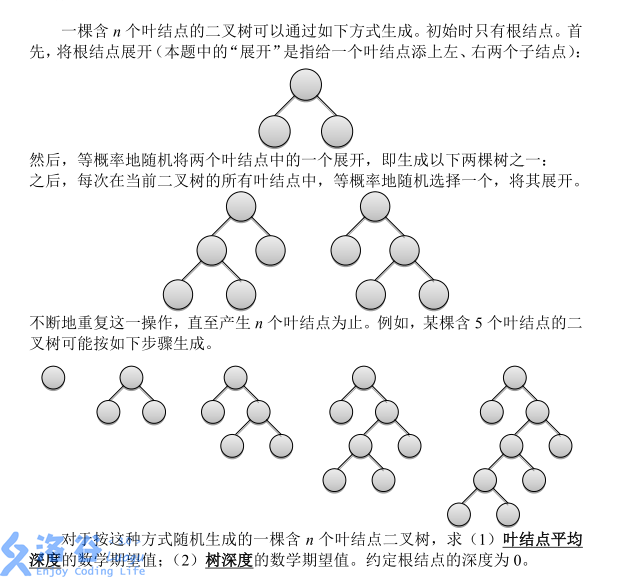
P3830 [SHOI2012]随机树

\(2\le n\le 100\)

第一问

比较简单，设 \(f_i\) 表示 \(i\) 个点的树的叶节点平均深度的期望，转移

\[f_i=\dfrac 1 x(f_{i-1}\times (i-1)+f_{i-1}+2)=f_{x-1}+\dfrac 2 x \]

第二问

设 \(f_{i,j}\) 表示有 \(i\) 个叶子，深度 \(\ge j\) 的概率，转移时枚举左儿子叶子数

\[f_{i,j}=\dfrac{1}{i-1}\sum_{k=1}^{i-1}f_{k,j-1}+f_{i-k,j-1}-f_{k,j-1}\times f_{i-k,j-1} \]

只要有一边深度 \(\ge j-1\) 就行了，减掉两边都 \(\ge j-1\) 的，至于左子树的大小 \(k\)，取 \([1,i-1]\) 的概率都是相等的，所以直接除以 \(i-1\)。

P3058 [USACO12NOV]Balanced Cow Breeds G/S

给一个只有左右括号的字符串，然后用 H、G 两种字符来标记这个序列，所有标记 H 的括号可以组成一个正确的括号序列，所有 G 标记的括号也组成一个正确的括号序列，然后输出这种标记方案的总数 \(\bmod 2012\) 的值。

由于有两个标记，考虑分开记录，设 \(f_{i,j,k}\) 表示到第 \(i\) 个字符，打 H 标记的剩下 \(j\) 个 "("，打 G 标记的剩下 \(k\) 个 "(" 的方案数。

转移时判断是什么括号，然后分讨打 H 或 G 标记

如果是 "("
- H: \(f_{i,j,k}+=f_{i-1,j-1,k}\)
- G: \(f_{i,j,k}+=f_{i-1,j,k-1}\)
如果是 ")"
- H: \(f_{i,j,k}+=f_{i-1,j+1,k}\)
- G: \(f_{i,j,k}+=f_{i-1,j,k+1}\)

最后答案为 \(f_{n,0,0}\)，第一维可以滚动。

P4798 [CEOI2015 Day1]卡尔文球锦标赛

数位 dp

如果使用 dfs 写法，记忆化数组空间需要 \(O(n^2)\)，记录当前在第几位，以及前面填的数中最大是多少，但很可惜空间开不下，放个代码

Code

int dfs(int cur, bool lim, int pre)
{
    if(cur == n + 1) return 1;
    if(!lim && ~f[cur][pre]) return f[cur][pre];
    int res = 0, up = lim ? a[cur] : pre + 1;
    for(int i = 1; i <= up; i++)
        res = add(res + dfs(cur + 1, lim & (i == up), max(pre, i)));
    if(!lim) f[cur][pre] = res;
    return res;
}

考虑递推，用时间换空间，设 \(f_{i,j,0/1}\) 表示前 \(i\) 个数，最大值为 \(j\)，是否顶着上界的方案数。

转移时从 \(f_{i,j,0/1}\) 向后转移，讨论最后一个填什么

\[f_{i+1,j,0}+=f_{i,j,0}\times j+f_{i,j,1}\times (a_{i+1}-1) \\ f_{i+1,j+1,0}+=f_{i,j,0} \\ f_{i+1,j,1}+=f_{i,j,1}\ (a_{i+1}\neq j+1) \\ f_{i+1,j+1,1}+=f_{i,j,1}\ (a_{i+1}=j+1) \]

第一维可以滚动。

AT2087 Friction

给定一个 \(n\times m\) 的矩阵，矩阵上每个格子都有一个小写字母表示颜色，每次操作可以选择一列向下推一格，然后最下面的格子会消失，操作一次的代价为操作前这一列中与旁边格子颜色相同的对数。

求将整个矩阵全消掉所需要的最小代价。

\(1\le n \le 300,2\le m\le 300\)

首先有个性质，任意相邻的两列的代价相互独立，也就是相邻两列的贡献可以单独算。

证明：考虑消掉三列的代价，相邻两列间相对操作顺序是不受第三列的影响的，并且两列如果不相邻是不会产生贡献的，所以代价可以单独计算。

接下来就是简单 dp 了，设 \(f_{i,j}\) 表示第一列还剩 \(i\) 个格子，第二列还剩 \(j\) 个格子消完的代价。

\[f_{i,j}=min(f_{i-1,j},f_{i,j-1})+w(i,j) \]

其中 \(w(i,j)\) 表示这个状态下的代价，可以递推出来，假设当前在算第 \(x\) 列和第 \(y\) 列的贡献

\[w(i,j)=w(i-1,j-1)+[s_{i,x}==s_{j,y}] \]

于是就可以 \(O(n^2m)\) dp 了。

CF327E Axis Walking

给你一个长度为 \(n\ (1\le n\le 24)\) 的正整数序列 \(S\)，再有 \(k\ (0\le k\le 2)\) 个正整数。

求有多少种 \(S\) 的排列方式使得其前缀和不会成为那 \(k\) 个数里的任意一个。答案对 \(10^9+7\) 取模。

看到 \(n\le 24\) 不难想到状压，设 \(f(S)\) 表示当前已经确定的数为 \(S\)，转移时枚举一个没有在 \(S\) 中的数 \(i\)，并判断 \(sum(S)+a_i\) 是否合法。

这样复杂度是 \(O(2^nn)\)，理论上 3s 是能过的，但是由于这是远古 CF 题，时限减半没能卡过去，考虑换一种转移方式。

对于一个状态 \(S\)，我们可以枚举最后一个数是多少，然后从前面的状态转移过来，这个可以用 \(lowbit\) 优化，常数极小，可以通过。

P3451 [POI2007]ATR-Tourist Attractions

给出一张有 \(n\) 个点 \(m\) 条边的无向图，每条边有边权。

你需要找一条从 \(1\) 到 \(n\) 的最短路径，并且这条路径在满足给出的 \(g\) 个限制的情况下可以在所有编号从 \(2\) 到 \(k+1\) 的点上停留。

每个限制条件形如 \(r_i, s_i\)，表示停留在 \(s_i\) 之前必须先在 \(r_i\) 停留过。

注意停留不等于经过。

\(2\le n\le2\times10^4\)

\(1\le m\le2\times10^5\)

\(0\le k\le\min(20, n-2)\)

\(2\le r_i, s_i\le k+1, r_i\not=s_i\)

观察到 \(k\) 很小，依然可以状压，所以思路就很清晰了

先对这 \(k\) 个点跑一遍最短路，设 \(f_{S,i}\) 表示从 \(1\) 出发，已经在 \(S\) 中的点停留过，最后待在 \(i\) 的最短路，转移时枚举不在 \(S\) 中的 \(j\)，要先判断能否在 \(j\) 停留，这个对每个点存一个需要的状态即可。

这样做空间复杂度是 \(O(2^nn)\) 的，大概是 80MB 左右，并不能过，需要卡空间。

其实差的并不多，只需要把 \(i\) 在 \(S\) 中去掉，也就是当前在 \(i\) 节点，那么状态里就不要存是否有 \(i\)，这样空间就是 \(O(2^{n-1}n)\) 了。

标签：le,颜色,好题,times,枚举,序列,转移,dp
来源： https://www.cnblogs.com/acestar/p/16436147.html