AcWing 98. 分形之城

题目传送门

一、理解题意

本题看懂题目花费了大量的时间，后面理解题意如下：
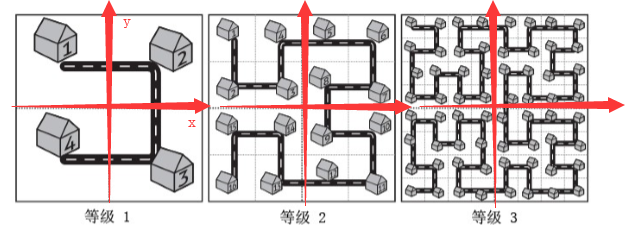
等级一：\(4\)个点,等级二: \(16\)个点,等级三:\(64\)个点... 至于贯穿这些点的线，是城市编号增长的顺序。

分析从等级一如何到等级二,原来的城区设为\(A\):

• \(A\)顺时针旋转\(90\)度,再关于中间线翻转一下得到等级二的左上角城区
• \(A\)向右平移得到右上角的城区
• \(A\)向右平移再向下平移得到右下角的城区
• 至于左下角城区，一会再说。

二、数学知识

我们知道，两点之间距离的平方是对应横纵坐标距离之差的平方和。
欧几里得距离

坐标旋转公式：比如第一象限的点(\(1,2\))，顺时针旋转\(90\)度得到的点在第四象限，也就是(\(2，-1\))，逆时针旋转\(90\)度得到的点在第二象限，也就是(\(-2,1\))。更一般的，(\(x，y\))顺时针旋转\(90\)度得到(\(y，-x\))，逆时针得到 (\(-y，x\))。

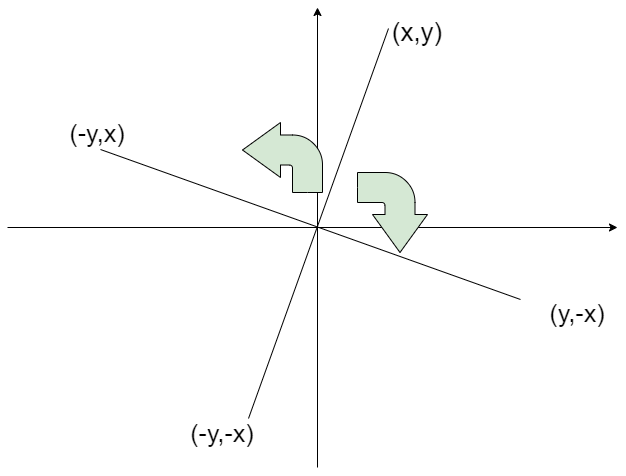
最重要的是确定坐标原点以及坐标系，大多数人都是按照二维数组的思想，把左上角第一个点作为原点，往下的方向作为\(x\)轴正方向，往右的方向作为\(y\)轴正方向，然后旋转都是绕左上角第一个点旋转，这样造成的问题就是左下角的城区在计算坐标时，逆时针旋转会转偏了，不容易计算。

个人浅见是按照各个等级城区中心为坐标原点:

刚开始一直是以城区一的中心为原点，然后图一的四个点坐标分别为：\((-1,1),(1,1),(1,-1),(-1,-1)\)

• 左上角：\((x,y)\)关于原点顺时针\(90\)度旋转得到\((y,-x)\)再关于\(y\)轴轴对称变换得到\((-y,-x)\)；
• 右上角：\((x,y)\)向右平移\(2*len\)个单位得到\((x+2*len,y)\)，注意这里的\(len\)在代码中有定义；
• 右下角：\((x,y)\)向右平移\(2*len\)个单位得到\((x+2*len，y)\)再向下平移\(2*len\)个单位得到\((x+2*len，y-2*len)\)；
• 左下角：\((x,y)\)逆时针旋转\(90\)度得到 \((-y,x)\)，再关于\(y\)轴轴对称变换得到\((y,x)\)，注意这里四个点的中心是旋转中心，所以只是换了方向，本质四个点还在原地，最后再向下平移\(2*len\)得到\((y，x-2*len)\).

以上是以第一行第一列的点为坐标原点(旋转中心)经坐标变换得到其他城区的点的，但是并不能\(ac\)，因为图一这样旋转变换得到图二没问题，但是图二绕原来的旋转中心再转就会转歪，后面坐标便不对了。解决办法就是一轮坐标变换后便改变坐标原点(旋转中心)，比如等级一经坐标变换后得到等级二的四个坐标后，立刻调整坐标原点(旋转中心)为等级二的中心，再推出等级三坐标，继续调整坐标原点，以此类推。

上面的调整坐标原点是向右下角移动，具体操作为调整原来的坐标，横坐标减小\(len\)，纵坐标增加\(len\)，也就是在上面推出的坐标后面对横纵坐标再次变换，注意必须先坐标转换再移动坐标原点，即得到:

• 左上角：\((-y，-x)\)改变坐标得到\((-y-len，-x+len)\)；
• 右上角：\((x+2*len，y)\)变成\((x+len，y+len)\)；
• 右下角：\((x+2*len，y-2*len)\)变成 \((x+len，y-len)\)；
• 左下角：\((y，x-2*len)\)变成\((y-len，x-len)\).

注意点：
1.代码中坐标公式是两步得到，第一步旋转平移，第二步移动原点。
2.虽然主题代码和\(yxc\)大佬一样，但是输出时是乘以\(5\)，看上面我写的关于等级一的四个坐标便可理解，原点不同。

三、实现代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> PII;

PII calc(LL n, LL m) {
    if (n == 0) return {0, 0}; //递归边界
    LL len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
    PII pos = calc(n - 1, m % cnt); //上一个等级的坐标信息
    LL x = pos.first, y = pos.second;
    LL z = m / cnt; //处在城区的哪个角
    if (z == 0) return {-y - len, -x + len};
    if (z == 1) return {x + len, y + len};
    if (z == 2) return {x + len, y - len};
    return {y - len, x - len};
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        LL N, A, B;
        cin >> N >> A >> B;
        PII ac = calc(N, A - 1);
        PII bc = calc(N, B - 1);
        double x = ac.first - bc.first;
        double y = ac.second - bc.second;
        printf("%.0lf\n", sqrt(x * x + y * y) * 5);
    }
    return 0;
}

四、疑问解答

\(Q\):有点不理解为啥需要\(10/2=5\)啊？
答：你认真看一下上面的第\(2\)张图，原来\(1\)，\(2\)小房子中间的距离是\(len=10\),现在，我们硬生生在它俩中间放上了原点，就相当于把原来的图给细化了一倍,原来的坐标(指以左上角为坐标原点时)\((0,0)\),\((0,1)\)给变成了\((-1,1)\),\((1,1)\),那么边长变可以理解为缩短了一半\(len=10/2=5\)

标签：原点,len,旋转,98,分形,坐标,得到,等级,AcWing
来源： https://www.cnblogs.com/littlehb/p/16419061.html