Andrew Ng ML课程SVM部分学习记录——SVM核函数

核函数

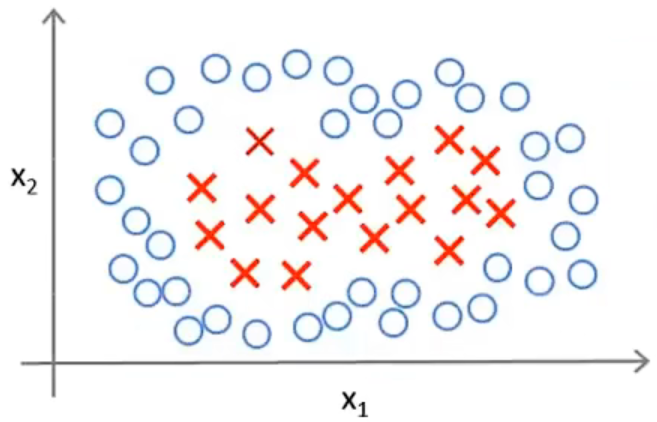
对于线性不可分的情况，可以借助核函数构造非线性分类器.

先选定部分标记点(landmarks)

对于一个样本\(x\)，设\(f\)度量样本与标记点的相似度：

\[f_1={\mathbf {similarity}}(x,l^{(1)})=\exp(-\frac{\parallel x-l^{(1)}\parallel^2}{2\sigma^2})\\ f_2={\mathbf {similarity}}(x,l^{(2)})=\exp(-\frac{\parallel x-l^{(2)}\parallel^2}{2\sigma^2})\\ f_3={\mathbf {similarity}}(x,l^{(3)})=\exp(-\frac{\parallel x-l^{(3)}\parallel^2}{2\sigma^2})\\ \cdots \]

这样的相似度函数被称作核函数，这里使用的是高斯核函数(Gaussian kernel function)，实际上一眼就能看出这和高斯分布密度函数长得很像。
当\(x\rightarrow l^{(1)}\)时：

\[\lim_{x\rightarrow l^{(1)}}f_1=\exp(0)=1 \]

当\(\parallel x-l^{(1)}\parallel\gg 0\)时：

\[\lim f_1=\exp(-\infty)=0 \]

核函数的图像如下，分别对应\(\sigma=1,\sigma=2,\sigma=3\)的情况

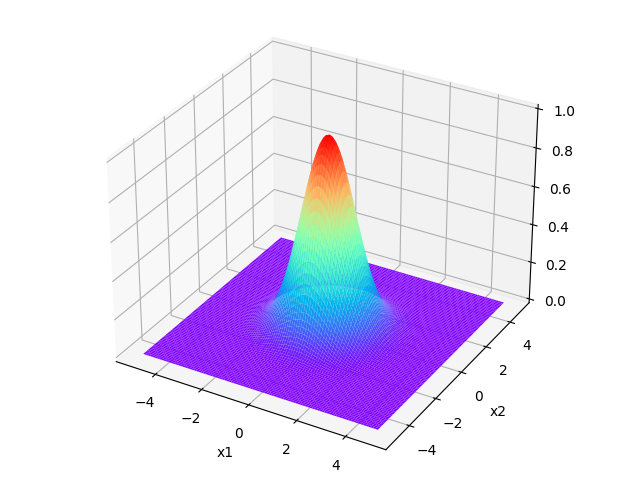
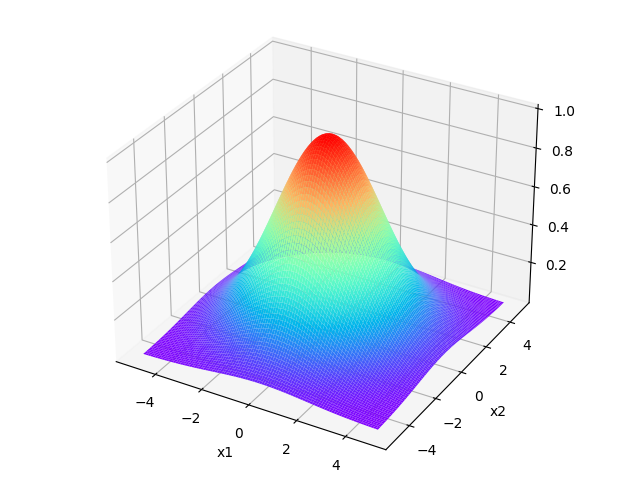
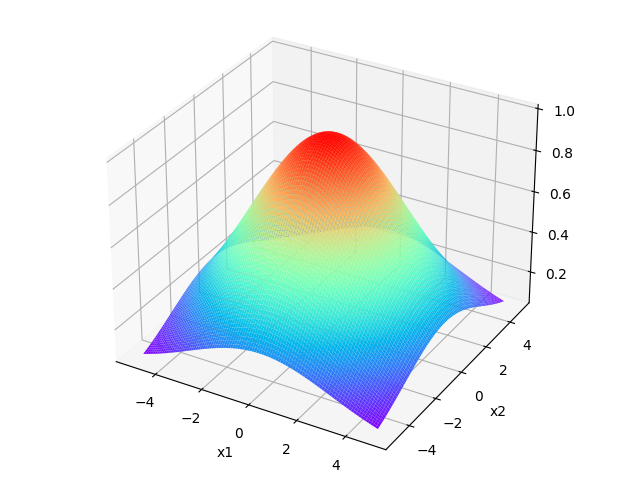
可以看出\(\sigma\)的值越大时，函数值（相似度）的下降越缓慢。

标签：SVM,mathbf,函数,similarity,ML,Andrew,exp,sigma,parallel
来源： https://www.cnblogs.com/allegro-vivace/p/16409663.html