LCT 学习笔记

还在更新……

看看学弟们几天后会把 LCT 给卷了：cntnow = 0

LCT 好难啊呜呜呜

这 LCT，尤其是 makeroot 中的区间翻转一步，根本不是人想到的。

虽然 Splay 也不是人想到的。

写了一些忽然发现网上有写的很好的了，那就这样，图直接放人家的，主要用来存代码方便背代码（

再写这样的对话几次后干脆给这两人取个正式点的名字吧（突发奇想

---

引入

A：让我们开始吧。从问题引入：在线维护一个森林，有连边、断边、查询两点路径的操作。如果这是一个静态问题，你会怎么操作？

B：无断边加边，这就是树剖模板。

A：为什么要用树剖呢？

B：往上跳时若当前非其重儿子，即换了一条链，子树大小至少*2，保证任意点到根至多换log条链。链的存储连续，这让我们可以用其它数据结构维护序列。

A：我们是怎么把树剖开的呢？

B：通过人工挑选“重儿子”

A：开始引入第一对概念：“实儿子”与“虚儿子”。每个节点都有唯一的“实儿子”。这样，树就被剖分成若干链了。用什么维护链比较好呢？

B：既然上链还动态了，当然用平衡树了！

---

辅助树

A：来介绍 LCT 的核心 - 辅助树。

之前说过，我们使用 Splay 分别维护树上每条链

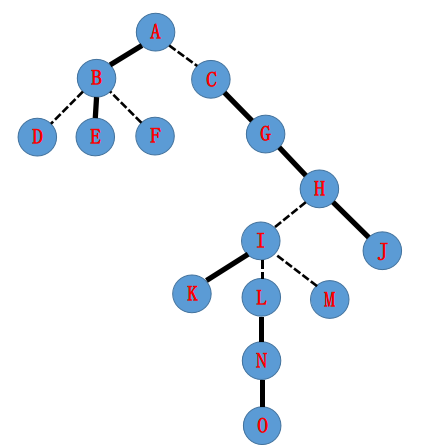
（图源：https://www.cnblogs.com/flashhu/p/8324551.html，后面还会引这里的图）

剖好后长后面这个样。

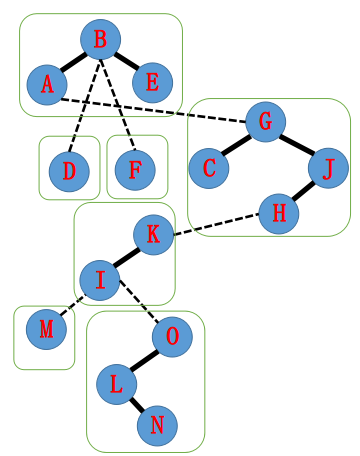
这棵树有些可爱的小性质，参照第一张图上的轻重链看。

B：

• 每条重链构成一棵 Splay，中序遍历后在原树对应从上到下那条链。
• 每棵 Splay 的根节点的根连向该链最上部的节点原树上的父亲
• 通过辅助树能唯一还原原树那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

A：最后一条告诉我们不用管原树，就管改辅助树。该上操作了。

为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

---

警告&声明

在以后的阅读请分清操作在原树还是在辅助树上。虽然我们只操作辅助树，很多时候会叙述这对原树的宏观影响。

“断***”相当于把这条边由实边变为虚边。

Splay 相关数组声明与宏定义

A：既然与 Splay 相关，直接看代码吧。

#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
#define isroot(x) (ch[fa[x]][0] != x && ch[fa[x]][1] != x)
int sz[M], rt, tot, fa[M], ch[M][2], val[M], cnt[M];
void pushup(int x) {sz[x] = sz[ls(x)] + sz[rs(x)] + cnt[x];}
bool get(int x) {return x == rs(fa[x]);}

pushup：字面意思

isroot：是否是辅助树中所在 Splay 的根

get：是 fa 的哪边儿子

特殊的 rotate

A：记得 rotate 吗……

因为认父不认子，我们需要对 rotate 做改造。

old version

void rotate(int x){ 
	int y = fa[x], z = fa[y], chk = get(x);
	ch[y][chk] = ch[x][chk ^ 1]; if(ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y; //处理 x 另一方向的儿子 
	fa[y] = x; ch[x][chk ^ 1] = y; fa[x] = z; //yx 父子关系对调 
	if(z) ch[z][y == ch[z][1]] = x; //xz 连边 
	pushup(x); pushup(y); 
}
void splay(int x, int goal){ //使 x 为 goal 儿子 
	while(fa[x] != goal){ //相当于判 x 是否到达
		int y = fa[x], z = fa[y];
		if(z != goal) //相当于判 y 是否到达
            rotate(get(x) == get(y) ? y : x);
		rotate(x);
	} if(!goal) rt = x;
}

z 是 x 的父亲的父亲。y 实际上不是 x 的父亲的可能可以排除，因为在外部的 splay 中会有检查。现在只需看 z 实际上是不是 x 的父亲。

void rotate(int x){ 
	int y = fa[x], z = fa[y], chk = get(x);
    if (!isRoot(y)) ch[z][ch[z][1] == y] = x; //特殊的 xz 连边
	ch[y][chk] = ch[x][chk ^ 1]; if(ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y; //处理 x 另一方向的儿子 
	fa[y] = x; ch[x][chk ^ 1] = y; fa[x] = z; //yx 父子关系对调 
	pushup(x); pushup(y); 
}
void splay(int x){ //使 x 为所在 Splay 的根 
	while(!isroot(x)){ //所有 fa[x] == goal 均应改为 isroot(x)
		int y = fa[x];
		if(!isroot(y)) rotate(get(x) == get(y) ? y : x);
		rotate(x);
	}
}

access

A：access 用于构建一条原树上树根到给定点的实路径。

现在假设我们要让 root 到 N 构成实链。

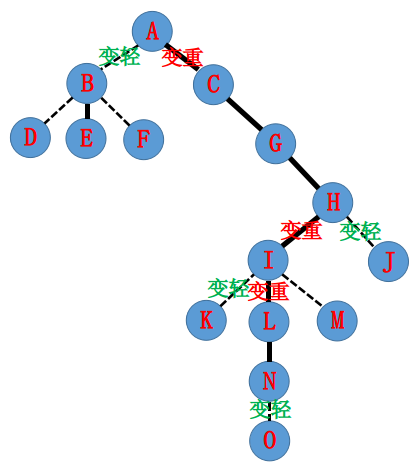
提示：从下到上。

B：第一步把 NO 间的边变轻。在辅助树上，只需让 O 成为 N 的直系儿子，然后让 N 不认 O，即可。因为 N 在辅助树上的 Splay 上仅在 N 后面，这可以通过 Splay(N) 实现。

A：下一步，需要断掉 IK 间的实边，因为一个节点只能有一个实儿子。

B：Splay(I) 后，K 就会成为 I 的右儿子。想要精准操控两个在原树中有父子关系的节点，只需要把其中一个转至所在 Splay 的根，另一个节点一定与其成辅助树上的父子关系。

此时递归下去即可。注意到上一段实际上是在构造 K 到根的路径，做下去即可。

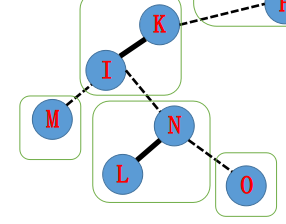
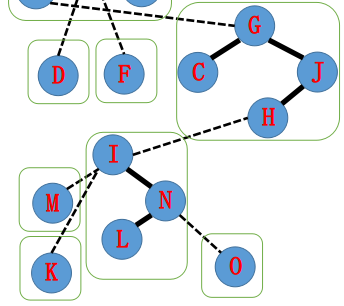
总结：旋转到所在 Splay 的根，断右子树，更新信息，转移到当前节点的 fa 做下去。

void access(int x){
    for(int f = 0; x; x = fa[x], f = fa[x]){
        splay(x); ch[x][1] = 0; pushup(x);
    }
}

---

makeroot

A：有时候，我们需要直接处理树上两点间的路径。找到 LCA 肯定不是最佳方法，我们希望这两个点能构成祖孙关系。

B：让其中一点成为原树上的根，另一点自然是它的晚辈。

A：所以，我们需要让 x 成为原树上深度最小的节点。这怎么做呢？

B：Splay 可以区间翻转，翻转过的区间的相对位置不变，如果翻转一条链呢？

A：问题不大。只有存储在这条链上的信息会改变，其它链的信息不会变，也就是所有链的父亲也不会变，对于它们来说，拓扑结构也不会变。只是对于翻转的那条链原来的父亲来说会有点麻烦。有什么好方法避免吗？

B：只要翻转的链含有根节点，就一切解决了。所有链的父亲节点不变，拓扑结构不变。一遍翻转后，原来最下面的节点事实上成为了新根。

access x 后把 x 旋到根

A：那就可以上代码了：

---

A：makeroot x？

A：link x y 连边？首先给出判定。

B：使用 findroot 判定，然后使用 makeroot(x); makeroot(y); 后直接 \(y\) 对 \(x\) 连虚边。

标签：Splay,LCT,ch,int,chk,笔记,学习,fa,节点
来源： https://www.cnblogs.com/purplevine/p/16388164.html