793div2 D

首先考虑满足边的奇偶性条件。

如果 \(\texttt{1}\) 的数量为奇数显然无解，如果为偶数，就连接两个 \(\texttt{1}\) 之间的所有边。

比如 \(\texttt{1001001001110}\)，连接 \(1\leftrightarrow 2\leftrightarrow3\leftrightarrow4\)，\(7\leftrightarrow8\leftrightarrow9\leftrightarrow10\) 和 \(11\leftrightarrow12\)。

然后缩点，看成 \(6\) 个点，分别是 \((1\sim4),5,6,(7\sim10),(11\sim12),13\)。

此时每个点都满足奇偶性条件，如果想加边需要满足一个点一次性加两条边。

主要问题是不连通，考虑把其中一个 \(\texttt{100...001}\) 拆开，拆成 \(\texttt{1}\) 和 \(\texttt{0...001}\)，此时再按顺/逆时针串在一起即可。

如下图：

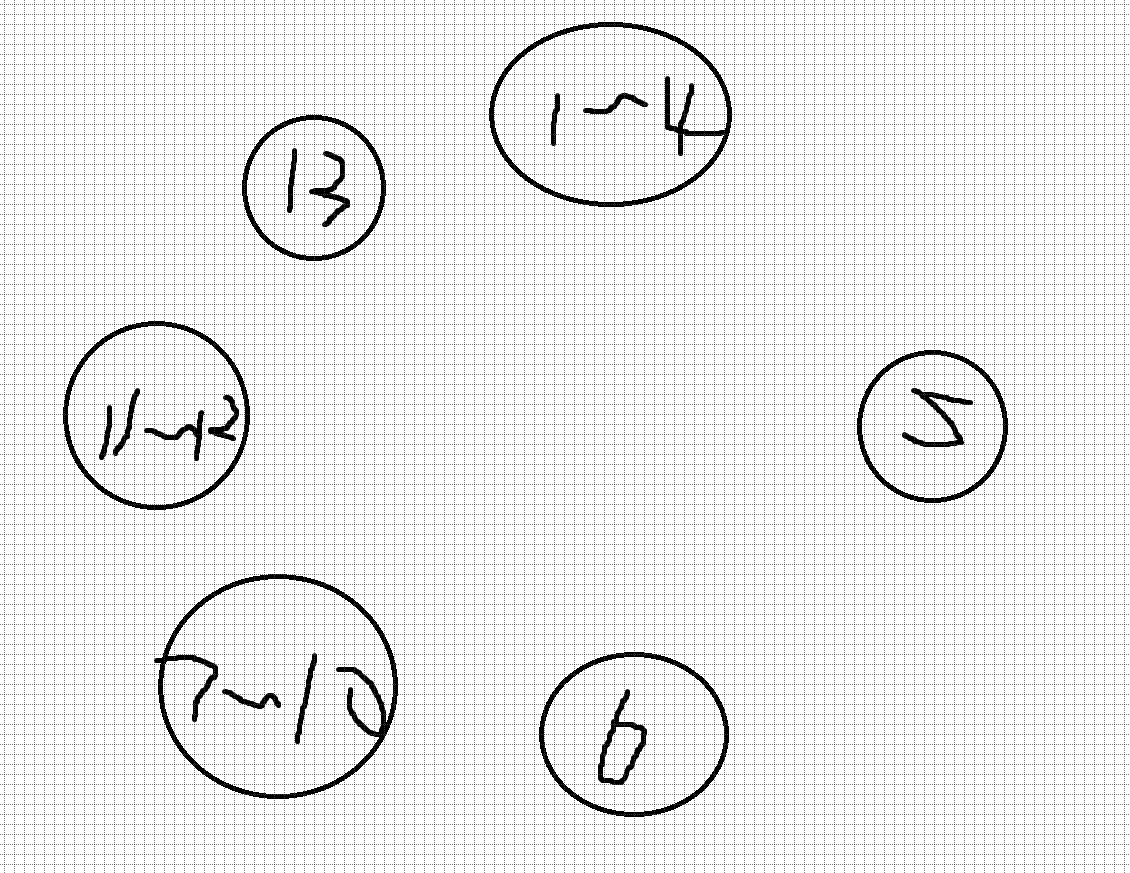
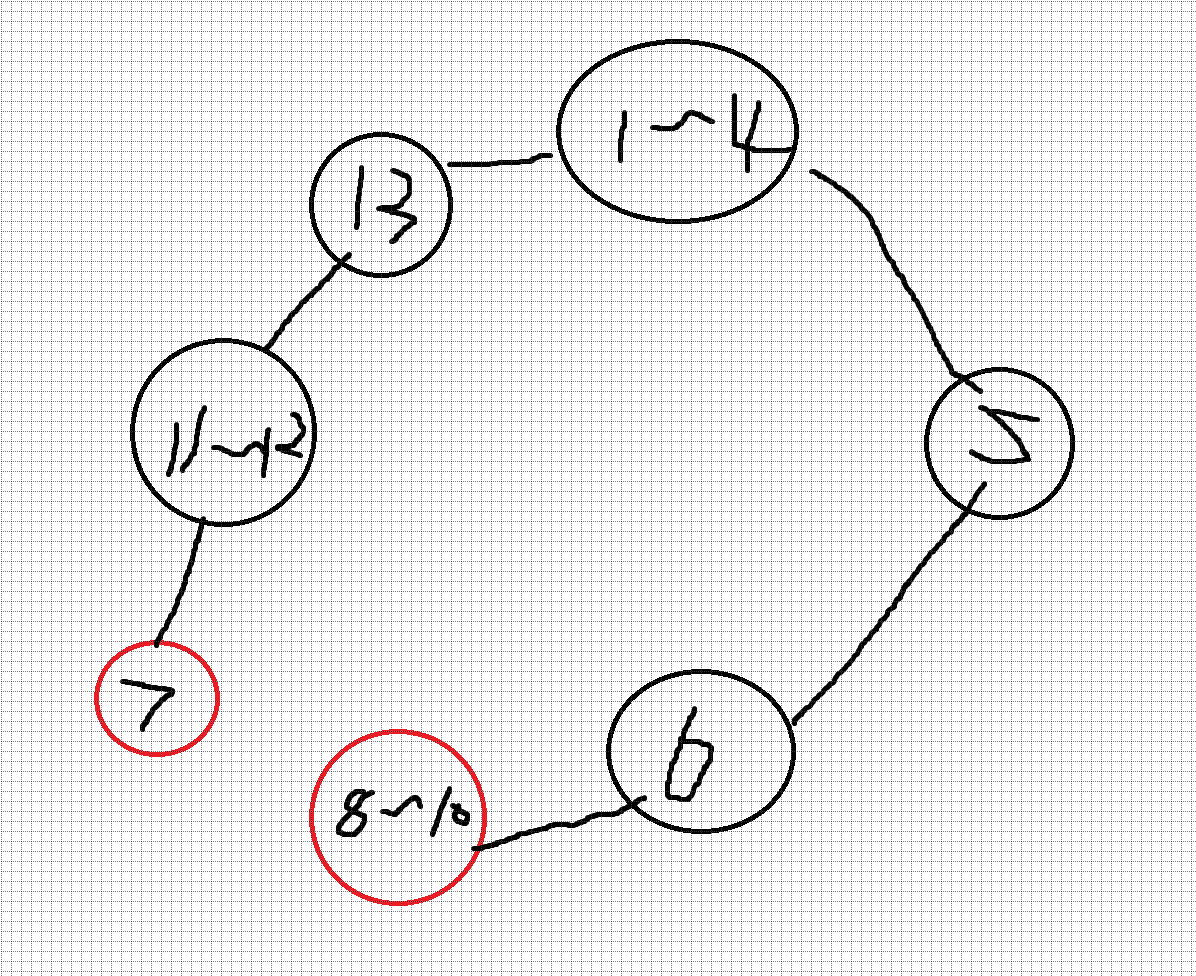
不难看出这个构造没有交叉。因为缩起来的点内部都是沿着圆周连接边的，不会对其他边产生可行性影响。并且你连的新边之间也没有交叉。

构造不了的情况就是没有点可以拆，即没有出现过 \(\texttt{1}\)，显然这种情况下无解，因为叶节点必须度数为 \(1\)，不可能没有奇数。

一些注意点：拆点后必须用原边连接的两个点去连其他点；对于一个缩点后的连通块，连接这个连通块的边必须连的是同一个点，比如上图 \(1\sim4\) 连在一起，用 \(5,13\) 两个点连接它的时候必须连同一个点，如 \((5,2),(13,2)\) 或 \((5,1),(13,1)\)，但是 \((5,1),(13,2)\) 是不合法的。因为奇偶性限制。

标签：...,13,793,连通,题解,texttt,CF,奇偶性,连接
来源： https://www.cnblogs.com/lingfunny/p/16361137.html