778. 水位上升的泳池中游泳(并查集)

778. 水位上升的泳池中游泳

在一个 n x n 的整数矩阵 grid 中，每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。

当开始下雨时，在时间为 t 时，水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。当然，在你游泳的时候你必须待在坐标方格里面。

你从坐标方格的左上平台 (0，0) 出发。返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间 。

示例 1:

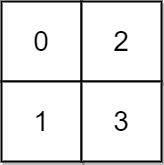
输入: grid = [[0,2],[1,3]]
输出: 3
解释:
时间为0时，你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

示例 2:

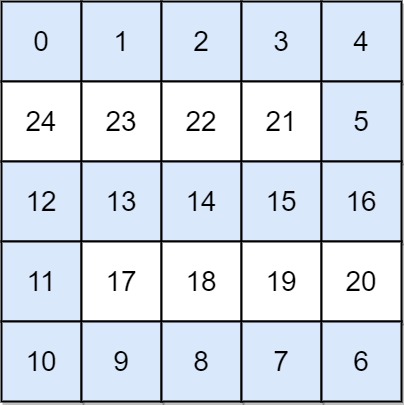
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释: 最终的路线用加粗进行了标记。
我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的

提示:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] < n2
• grid[i][j] 中每个值 均无重复

 1 class UinionFindeSet {
 2 public:
 3     // 初始化并查集,所有节点均指向自己(每个节点的根节点是自己)
 4     void init(int n) {
 5         parent.resize(n);
 6         for (int i = 0; i < n; i++) {
 7             parent[i] = i;
 8         }
 9         return;
10     }
11     // 获取与x连通的根节点
12     int findRoot(int x) {
13         int root = x;
14         while (root != parent[root]) {
15             parent[root] = parent[parent[root]];
16             root = parent[root];
17         }
18         return root;
19     }
20     // 两节点是否连通(在同一集合中)
21     bool isConnected(int x, int y) {
22         return (findRoot(x) == findRoot(y));
23     }
24     // 合并两节点
25     void unify(int x, int y) {
26         if (isConnected(x, y)) {
27             return;
28         }
29         parent[findRoot(x)] = findRoot(y);
30         return;
31     }
32 private:
33     vector<int> parent; // 储存每个节点对应连通的根节点
34 };
35 class Solution : public UinionFindeSet {
36 public:
37     // 上、左、下、右四个方向
38     vector<std::pair<int, int>> g_direction = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
39     unordered_map<int, int> hashMap; // key->方格中平台的高度,value->方格的坐标(转换为一维坐标即节点值)
40     bool isInArea(int edge, int x, int y) {
41         return (x >= 0 && x < edge && y >= 0 && y < edge);
42     }
43     // 根据二维坐标获取一维坐标下标索引
44     int getIndex(int x, int y, int n) {
45         return (x * n + y);
46     }
47     int swimInWater(vector<vector<int>>& grid) {
48         if (grid.size() == 0) {
49             return -1;
50         }
51         int n = grid.size();
52         int length = n * n; // 节点个数
53         init(length);
54         // 1、初始化hash表,保存当前方格中水位高度与当前方格一维坐标的映射关系
55         for (int i = 0; i < n; i++) {
56             for (int j = 0; j < n; j++) {
57                 hashMap[grid[i][j]] = getIndex(i, j, n);
58             }
59         }
60         // 2、合并满足条件(此时水位必须同时淹没这两个平台)的相邻两个方格
61         for (int i = 0; i < length; i++) {
62             // 根据当前宫格水位高度i获取当前宫格的位置坐标
63             int curX = hashMap[i] / n;
64             int curY = hashMap[i] % n;
65             /*  向相邻宫格(四个方向)合并满足条件的宫格 
66             *   1、相邻宫格在矩阵边界内
67             *   2、相邻宫格水位的高度不大于当前水位高度(当前水位高的向相邻水位低的合并)
68             */
69             for (auto &pair : g_direction) {
70                 int nextX = curX + pair.first;
71                 int nextY = curY + pair.second;
72                 if (isInArea(n, nextX, nextY) && grid[nextX][nextY] <= i) {
73                     unify(hashMap[i], getIndex(nextX, nextY, n));
74                 }
75                 // 如果宫格合并后满足起点与终点连通,则返回当前宫格水位的高度(所需最少的时间)
76                 if (isConnected(0, length - 1)) {
77                     return i;
78                 }
79             }
80         }
81         return -1;
82     }
83 };

标签：parent,int,查集,778,水位,grid,方格,泳池,坐标
来源： https://www.cnblogs.com/MGFangel/p/16223024.html