[Acwing 164. 可达性统计] 题解报告

事实上，这道题并不需要拓扑排序。（当然，拓扑排序还是更快）

• 题目分析
  首先，题目中说了，这是一个有向无环图，所以，我们可以考虑 \(\texttt{DP}\) / 记搜 / 拓扑排序 来解决这道题。
  (我的做法是记忆化搜索。

• 雷区分析
  刚开始我用 \(f[i]\) 表示从 \(i\) 出发能够到达的点的个数，利用记忆化搜索更新状态。
  \(f[i] = f[枚举所有出边] + 1\)
  代码如下：

    #include <iostream>
    #include <cstring>
    #include <cstdio>
    #include <algorithm>
    
    using namespace std;
    
    const int N = 30010;
    
    int f[N];
    int n, m;
    int h[N], e[N], ne[N], idx;
    
    void add(int a, int b)
    {
        e[ ++ idx] = b, ne[idx] = h[a], h[a] = idx;
    }
    
    void dfs(int u)
    {
        if (f[u]) return;
        int s = 1;
        
        for (int i = h[u]; i; i = ne[i])
        {
            int j = e[i];
            dfs(j);
            s += f[j];
        }
        
        f[u] += s;
    }
    
    int main()
    {
        scanf("%d%d", &n, &m);
            
        for (int i = 1, x, y; i <= m; i ++ )
            scanf("%d%d", &x, &y), add(x, y);
        
        for (int i = 1; i <= n; i ++ )
            if (!f[i])
                dfs(i);
        
        for (int i = 1; i <= n; i ++ )
            printf("%d\n", f[i]);
            
        return 0;
    }

然鹅，我们没有考虑到一种情况，如图：

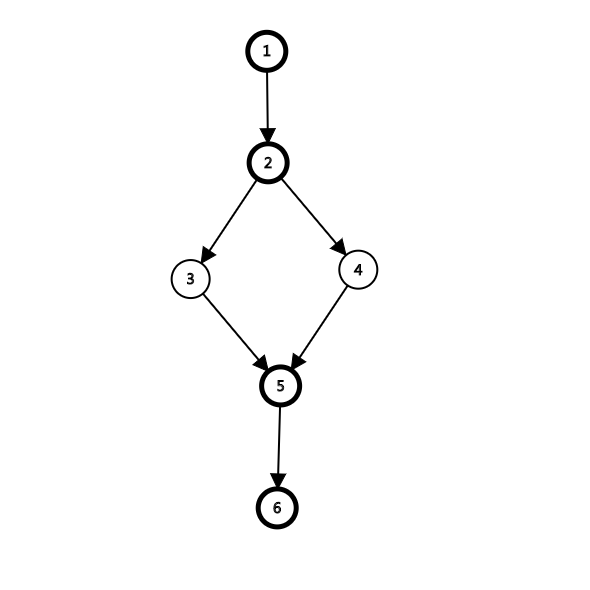
如果按照刚才上面的做法，那么 \(5, 6\) 号节点就会被统计两次，造成结果偏大。

所以，我们需要记录一下每个出点可到点的并集，这可以用 \(bitset\) 来实现

• \(bitset\) 用法

  1. \(bitset\) 可以实现二进制运算的 |, ^, & 等操作。
  2. \(bitset.any()\) 返回 \(bitset\) 中是否有 \(1\)
  3. \(bitset.none()\) 返回 \(bitset\) 中是否全为 \(0\)

• \(\texttt{Code}\)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <bitset>

using namespace std;

const int N = 30010;
int n, m; 
int h[N], e[N], ne[N], idx;
bitset<N> f[N];

void add(int a, int b)
{
	e[ ++ idx] = b, ne[idx] = h[a], h[a] = idx;
}

void dfs(int u)
{
	if (f[u].any()) return;
	
	f[u][u] = 1;
	bitset<N> s;
	
	for (int i = h[u]; i; i = ne[i])
	{
		int j = e[i];
		dfs(j);
		s |= f[j];
	}
	
	f[u] |= s;
}

int main()
{
	scanf("%d%d", &n, &m);
	
	while (m -- )
	{
		int a, b;
		scanf("%d%d", &a, &b);
		add(a, b);
	}
	
	for (int i = 1; i <= n; i ++ )
		if (f[i].none())
			dfs(i);
			
	for (int i = 1; i <= n; i ++ )
		printf("%d\n", f[i].count());
		
	return 0;
}

标签：idx,int,题解,void,ne,bitset,164,include,可达性
来源： https://www.cnblogs.com/LcyRegister/p/16185368.html