最短路问题的一些见解
作者:互联网
0x00. 最短路的定义
在一个赋权图 \(G\) 中,点 \(u\) 到点 \(v\) 有若干条通路,定义 \(u\) 到 \(v\) 的最短路为这些通路中边权值和最短的一条
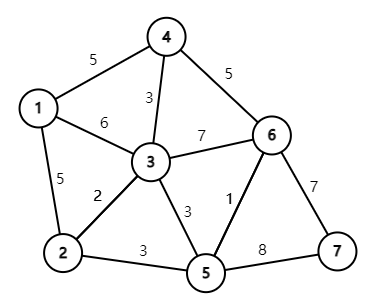
在上图中,从 \(1\) 到 \(7\) 的最短路为 \(1 \rightarrow 2 \rightarrow 5 \rightarrow 7\) 或者 \(1 \rightarrow 2 \rightarrow 5 \rightarrow 6 \rightarrow 7\),长度均为 \(16\)
(一般来讲我们都关注最短路的长度,部分题目会要求输出最短路的路径,这种情况依照题目要求进行取舍)
最短路问题分为单源最短路和多源最短路
单源最短路,顾名思义,就是求图 \(G\) 中一个结点(源点)到其他结点的最短路径
多源最短路,就是求图 \(G\) 中结点到其他结点的最短路径
概念
我们约定 dis[v] 为当前状态下源点到 \(v\) 的最短距离,D[v]为源点到 \(v\) 的实际最短距离
-
松弛(relax):对于一条边 \(e\{u,v,w\}\) (从 \(u\) 指向 \(v\),边权为 \(w\)),如果有 \(dis[v] > dis[u]+w\) ,则我们将 \(dis[v]\) 的值更新为 \(dis[u]+w\),这个过程称为对边的松弛
-
负环:若图中存在一个环,并且构成环的边的权值之和为负值,则称该环为一个负环
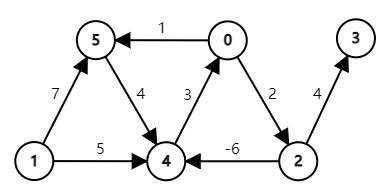
如图所示,环 \(0 \rightarrow 2 \rightarrow 4 \rightarrow 0\) 的边权和为 \(-1\) ,它是一个负环;与之相对,环 \(0 \rightarrow 5 \rightarrow 4 \rightarrow 0\) 的边权和为 \(8\) ,它不是一个负环。需要注意的是,有向图中具有负权边不代表着一定有负环,而无向图中具有负权边则一定有负环(因为负权边是双向的)
由于负环的特性,我们每经过一次负环,最短路的长度都会减小,直至负无穷。所以,在具有负环的图上讨论最短路是没有意义的
性质
- 最短路不经过重复的边,重复的顶点,即最短路不包含回路
- 含有 \(n\) 个结点的图 \(G\) (不包含负环)中,最短路最多包含 \(n-1\) 条边,最多包含 \(n\) 个结点
- 如果 \(u \rightarrow v\) 的最短路径经过结点 \(a,b\) ,则结点 \(a \rightarrow b\) 的最短路径是 \(u \rightarrow v\) 最短路径的一部分(最优子结构性)
- 正权图 \(G\) 中如果路径 \(s \rightarrow u \rightarrow v\) 中在松弛边 \(u \rightarrow v\) 之前 \(dis[u] = D[u]\) ,那么在松弛边 \(u \rightarrow v\) 之后有 \(dis[v] = D[v]\)(收敛性)
0x01. 最短路问题的建图方式
我们约定变量的含义
u表示边的起点
v表示边的终点
w表示边的边权
struct edge用来存储边的信息
剩下的自己猜
直接存边
用结构体数组直接存每一条边的起点,终点,边权
using ll = long long;
constexpr int maxn = 1e6+5;
constexpr int maxe = 1e6+5;
struct edge
{
ll u,v,w;
}e[maxe];
邻接矩阵
我们建立一个二维数组 e[maxn][maxn],规定 e[u][v] 的值为 \(u\) 到 \(v\) 的边权
using ll = long long;
constexpr int maxn = 1e3+5;
ll mp[maxn][maxn];
邻接表
我们对每一个结点建立一个vector,存从该节点出发的边及其边权
using ll = long long;
constexpr int maxn = 1e6+5;
struct edge
{
ll v,w;
};
vector<edge> mp[maxn];
链式前向星
本质上是通过链表的形式实现的邻接表,用于优化邻接表的大常数
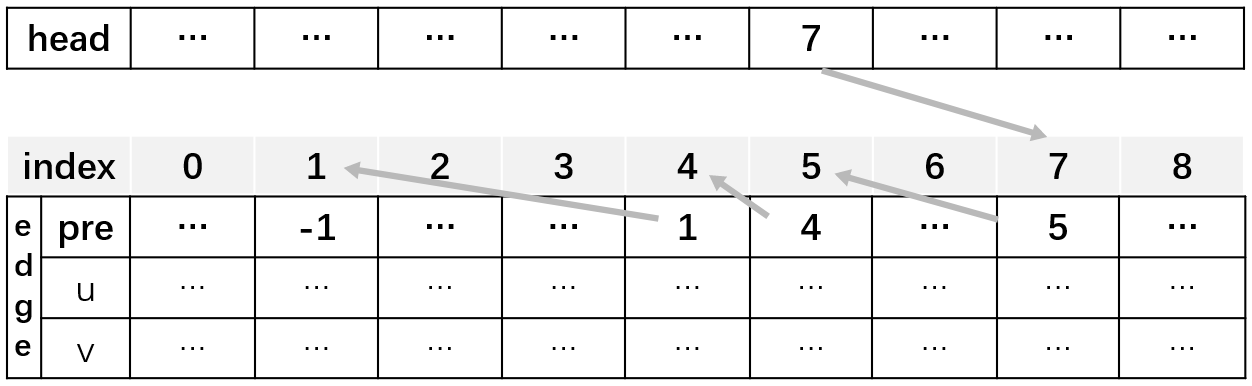
其思想是通过一个head数组来记录某一个结点的最新的相邻的边索引,根据索引来在记录边的e数组中访问最新的边,并通过边的pre变量来访问上一条邻边,如此递归,直到遍历完该点的所有邻边
using ll = long long;
constexpr int maxn = 1e6+5;
constexpr int maxe = 1e6+5;
struct edge
{
ll v,w;
int pre;
}e[maxe];
int head[maxn];
int ecnt(0);
inline void add(ll u,ll v,ll w)
{
e[ecnt].v = v;
e[ecnt].w = w;
e[ecnt].pre = head[u];
head[u] = ecnt++;
}
在以下的算法描述中,我们使用邻接表进行存图(因为好写(~ ̄▽ ̄)~)
0x02. 单源最短路
例题:单源最短路(模板)
Bellman-Ford算法
朴素
思想:基于松弛,每一次循环对图上的所有边进行松弛,当一次循环中没有一次松弛成功时退出循环。
由于每次循环我们都要遍历图上所有边,一次循环可以将最短路向前推进一个结点,而最短路最多有 \(n\) 个结点,所以该算法的时间复杂度为 \(O(nm)\)
我们也可以利用Bellman-Ford及其优化算法来判断负环,如果从源点出发能够到达负环(注意和图中有负环进行区分,如果负环不能从源点抵达,那么Bellman-Ford算法不能找出该负环,此时需要一些奇技淫巧),那么图上的边可以不断的被松弛,导致算法进入死循环,而我们知道最短路最多包含 \(n\) 个结点,只要循环超过了 \(n\) 次,那么就一定是碰上负环了。
代码:https://github.com/SirlyDreamer/Pastebin/blob/main/PlainBellmanFord.cpp
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
using ll = long long;
constexpr int maxn = 1e6 + 5;
struct edge
{
int v;
ll w;
} tmp;
vector<edge> mp[maxn];
ll dis[maxn];
bool Bellman_Ford(int cur, ll n)
{
//初始化dis数组
memset(dis, 0x3f, sizeof dis);
dis[cur] = 0;
bool ok(true); //标记当前轮是否成功进行一次松弛
int lim(n); //设置松弛轮数的限制,如果限制归零则说明有负环
while (lim-- && ok)
{
ok = false;
//遍历图中的所有边并松弛
for (int u(1); u <= n; ++u)
for (auto& [v,w] : mp[u])
/*C++17语法,等价于
for(int i(0); i < mp[u].size(); ++i)
{
int& v = mp[u][i].v;
ll& w = mp[u][i].w;*/
if (dis[v] > dis[u] + w) //对边{u,v,w}进行松弛操作
{
dis[v] = dis[u] + w;
ok = true;
}
}
return lim >= 0; //如果有负环则lim=-1,返回false
}
int main()
{
int m, n, s, t;
cin >> n >> m >> s >> t;
for (int i(0); i < m; ++i)
{
int u, v;
ll w;
cin >> u >> v >> w;
tmp.w = w;
tmp.v = v;
mp[u].push_back(tmp);
tmp.v = u;
mp[v].push_back(tmp);
}
Bellman_Ford(s,n);
cout << dis[t];
return 0;
}
如何优化?
通过观察可以发现,我们之前在松弛的过程中无外乎有三种情况:
-
\(dis[u] = \infin\) 时,\(dis[v]\) 此时的值无法更新或无意义更新,这次松弛是无效的
-
\(dis[u] \neq D[u]\) 时,\(dis[v]\) 此时的值虽然可以更新,但后续 \(dis[u]\) 也得到更新时,\(dis[v]\) 需要再次更新,这次松弛是多余的
-
\(dis[u] = D[u]\) 时,\(dis[v]\) 的值一旦确定,就不会再因为 \(dis[u]\) 的改变而更新,这次松弛是有效的
为了优化,我们就需要减少第一和第二种情况的发生,尽量让松弛变得有效
如何减少第一种情况捏?
通过观察我们发现,第一种情况发生在结点 \(u\) 还没有被访问到的时候,也就是说,只有 \(u\) 被访问过了,对 \(v\) 的松弛才是有意义的。
为了防止随机选择边松弛带来的时间浪费,我们可以从源点开始,将与刚刚访问过的结点 \(u\) 相连的结点 \(v\) 加入队列并标记,每次循环松弛与队首结点相连的边,这样就避免了第一种情况的发生。
这种优化后的算法,在OI界被称为
SPFA (Shortest Path Faster Algorithm)
SPFA算法的时间复杂度很是玄学,通常认为是 \(O(km)\) (\(k\)表示结点的平均入队次数)
代码:https://github.com/SirlyDreamer/Pastebin/blob/main/SPFA.cpp
#include <iostream>
#include <vector>
#include <cstring>
#include <queue>
using namespace std;
using ll = long long;
constexpr int maxn = 2505;
constexpr int maxm = 6205;
struct edge {
int v;
ll w;
} tmp;
vector<edge> mp[maxn];
int dis[maxn] = { 0 };
bool spfa(int u,int n) {
queue<int> T; //存储接下来需要更新dis的点
bool vis[maxn] = { false }; //标记是否在队列中
int cnt[maxn] = {0}; //统计访问点的次数,如果超过n则说明有负环
memset(dis, 0x3f, sizeof dis); //初始化dis数组为∞
dis[u] = 0;
T.push(u); //将源点入队并标记
vis[u] = true;
while (!T.empty()) {
u = T.front(); //取出队列前端的点并出队
T.pop();
vis[u] = false; //点u不在队列中了,标记为false
for (auto& [v, w] : mp[u]) {
if (dis[u] + w < dis[v]) { //松弛点u的出边
dis[v] = dis[u] + w;
if (!vis[v]) { //如果松弛成功则将边的终点入队
T.push(v);
vis[v] = true;
cnt[v]++; //统计入队次数(即松弛轮数),如果大于n则说明有负环
if(cnt[v] > n)
return false;
}
}
}
}
return true;
}
int main() {
ll m, n, s, t;
cin >> n >> m >> s >> t;
for (int i(0); i < m; ++i) {
ll u, v, w;
cin >> u >> v >> w;
tmp.w = w;
tmp.v = v;
mp[u].push_back(tmp);
tmp.v = u;
mp[v].push_back(tmp);
}
spfa(s,n);
cout << dis[t];
return 0;
}
可惜他在处理正权图时死了(

如何减少第二种情况捏?
我们希望每次松弛的边都能使其终点 \(v\) 的 \(dis[v]\) 被更新成其真实最短路。
我们可以用贪心的思想来做,需要注意的是,这种贪心的思想仅在没有负权边的情况下成立,假设在算法运行的过程中,结点有两种情况:点集 \(S\) 中的点已经确定了其最短路长度,点集 \(T\) 中的点则没有。
如果我们从 \(T\) 中选取一个点 \(u\),其当前最短路 \(dis[u]\) 在点集 \(T\) 中最小,此时 \(dis[u] = D[u]\)(收敛性,正确性证明),我们将其加入点集 \(S\) ,并松弛其所有出边.
当集合 \(T\) 为空时结束
这是啥捏,这就是大名鼎鼎的
Dijkstra 算法
Dijkstra算法的时间复杂度实际上很是取决于在 \(T\) 中寻找最小的 \(dis[u]\),如果我们采用遍历 \(O(n)\) 查找的方法,其总的时间复杂度为 \(O(n^2)\),如果我们使用优先队列进行优化,则其时间复杂度可以达到 \(O(m \space \log m)\)
代码:https://github.com/SirlyDreamer/Pastebin/blob/main/Dijkstra.cpp
#include <iostream>
#include <vector>
#include <cstring>
#include <queue>
using namespace std;
using ll = long long;
constexpr int maxn = 2505;
constexpr int maxm = 6205;
struct edge {
ll w;
int v;
bool operator<(const edge b) const { return w > b.w; } //定义排序方式
} tmp;
vector<edge> mp[maxn];
int dis[maxn] = { 0 };
void dij(int u) {
priority_queue<edge> T; //这里并不是存边,这里存的是当前状态下,某一点和他的dis
//由于刚好又是边的两个参数,所以偷了个懒,直接拿边的struct来顶上了qwqwqwq
bool vis[maxn] = { false }; //区分S点集和T点集,当vis[u] == true时我们认为u在S点集中
memset(dis, 0x3f, sizeof dis); //初始化dis数组,并将源点设置成0
dis[u] = 0;
T.push({ 0, u }); //将源点及其距离推入队列
while (!T.empty()) {
u = T.top().v; //取出优先队列中当前dis最小的点
T.pop();
if (vis[u]) //如果这个点已经访问过则忽略这个点
continue;
vis[u] = true; //将其加入S点集
for (auto &[w, v] : mp[u]) { //松弛其所有出边,并将其终点和dis加入优先队列
if (dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
T.push({ dis[v], v });
}
}
}
}
int main() {
int m, n, s, t;
cin >> n >> m >> s >> t;
for (int i(0); i < m; ++i) {
int u, v;
ll w;
cin >> u >> v >> w;
tmp.w = w;
tmp.v = v;
mp[u].push_back(tmp);
tmp.v = u;
mp[v].push_back(tmp);
}
dij(s);
cout << dis[t];
return 0;
}
好了,单源最短路问题的常用算法就这些了,我们现在来做一个总结
| 算法 | 朴素Bellman-Ford | SPFA | Dijkstra |
|---|---|---|---|
| 适用范围 | 无负环的图 | 无负环的图 | 正权图 |
| 时间复杂度 | \(O(nm)\) | \(O(km)\) | \(O(m \log m)\) |
| 能否检测负环 | 能检测 | 能检测 | 不能检测 |
| 图规模 | 小 | 中/大 | 中/大 |
0x03. 多源最短路
多源最短路 = 跑n次单源最短路(bushi
其实是可以的,在某些图上跑n次单源最短路还不算慢
这里我们介绍一下
Floyd算法
基于动态规划,我们定义一个数组 f[k][x][y],表示只允许经过结点 \(1\) 到 \(k\) 所构成的子图,结点 \(x\) 到结点 \(y\) 的最短路长度。
显然,f[n][x][y] 就是结点 \(x\) 到结点 \(y\) 的最短路长度。
状态转移方程:f[k][x][y] = min(f[k-1][x][y], f[k-1][x][k] + f[k-1][k][y])
通过观察得知,我们可以去掉第一维以优化空间复杂度
代码:https://github.com/SirlyDreamer/Pastebin/blob/main/Floyd.cpp
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
using ll = long long;
constexpr int maxn = 2505;
constexpr ll inf = 0x3f3f3f3f3f3f3f3fL;
ll dis[maxn][maxn];
int main() {
int n, m, t;
cin >> n >> m >> t;
memset(dis, 0x3f, sizeof dis);
for (int i(0); i <= n; ++i)
dis[i][i] = 0; //初始化,自己到自己的最短路为0
for (int i(0); i < m; ++i) {
int u, v;
ll w;
cin >> u >> v >> w;
dis[u][v] = dis[v][u] = w; //这里我们偷懒不存边,我们直接把u和v之间的最短路更新成其边权
//如果有重边的话这里需要取其最小值
}
for (int k(1); k <= n; ++k) //k要写在最外层!!!!
for (int i(1); i <= n; ++i)
for (int j(1); j <= n; ++j)
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]); //状态转移
for (int i(0); i < t; ++i) {
int u, v;
cin >> u >> v;
if (dis[u][v] == inf)
cout << "-1\n";
else
cout << dis[u][v] << "\n";
}
return 0;
}
这就完了?这就完了(๑•̀ㅂ•́)و✧
标签:见解,int,短路,结点,maxn,一些,ll,dis 来源: https://www.cnblogs.com/SirlyDreamer/p/16096964.html