机器学习（2）-- 衡量回归的性能指标

衡量回归的性能指标

机器学习通常都是将训练集上的数据对模型进行训练，然后再将测试集上的数据给训练好的模型进行预测，最后根据模型性能的好坏选择模型，对于分类问题，大家很容易想到，可以使用正确率来评估模型的性能，那么回归问题可以使用哪些指标用来评估呢？

1. $ MSE $ (均方误差) :
   \[\frac{1}{m} {\textstyle \sum_{i=1}^{m}}(y^{i}-p^{i})^{2} \]

• \(y^{i}\) 表示第\(i\)个样本的真实标签，\(p^{i}\)表示模型对第\(i\)个样本的预测标签。线性回归的目的就是让损失函数最小。那么模型训练出来了，我们在测试集上用损失函数来评估模型就行了。

2. \(RMSE\)(均方根误差) :

\[\sqrt{\frac{1}{m} {\textstyle \sum_{i=1}^{m}}(y^{i}-p^{i})^{2}} \]

2. \(MAE\) (平均绝对误差) :

\[\frac{1}{m} {\textstyle \sum_{i=1}^{m}} \left | y^{i}-p^{i} \right | \]

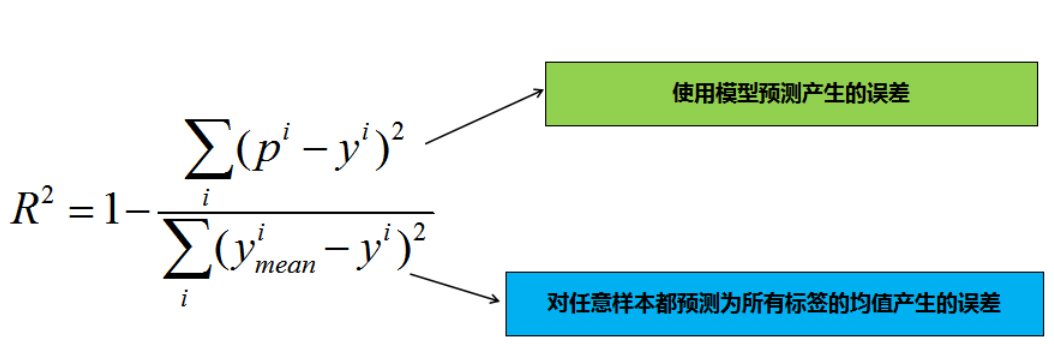
2. \(R-Squared\) :
   \[R^{2} = 1 - \frac{\sum_{i}^{} (p^{i} - y^{i}) ^{2}}{\sum_{i}^{}(y_{mean}^{i} - y^{i})^{2} } \]

• 其中\(Y_{mean}\)表示所有测试样本标签值的均值（其实分子表示的是模型预测时产生的误差，分母表示的是对任意样本都预测为所有标签均值时产生的误差）

准确度的陷阱与混淆矩阵

准确度：

• 准确对越高就能说明模型的分类性能越好吗？非也！

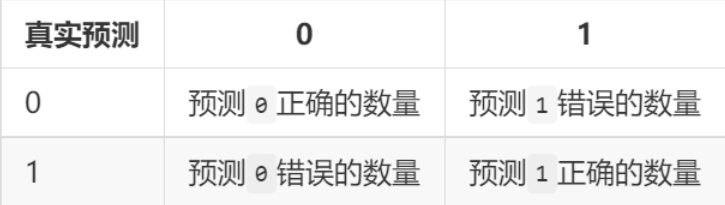
混淆矩阵：（意义）

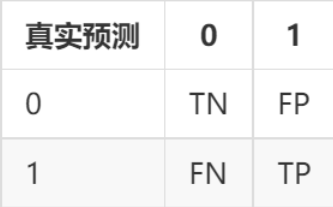
如果将正确看成是 \(True\)，错误看成是 \(False\)， \(0\) 看成是 \(Negtive\)， \(1\) 看成是 \(Positive\)。然后将上表中的文字替换掉，混淆矩阵如下：

所以模型分类性能越好，混淆矩阵中非对角线上的数值越小。

精准率与召回率：

精准率(Precision) 指的是模型预测为 Positive 时的预测准确度，其计算公式如下：

\[Precision = \frac{TP}{TP+FP} \]

• 精准率越高，那么癌症检测系统预测某人患有癌症的可信度就越高。

召回率(Recall) 指的是我们关注的事件发生了，并且模型预测正确了的比值，其计算公式如下：

\[Recall = \frac{TP}{TP+FN} \]

• 召回率越高，那么我们感兴趣的对象成为漏网之鱼的可能性越低。

模型的精准率变高，召回率会变低，精准率变低，召回率会变高。

到底应该使用精准率还是召回率作为性能指标，其实是根据具体业务来决定的。

比如我现在想要训练一个模型来预测我关心的股票是涨($ Positive$ )还是跌( \(Negtive\) )，那么我们应该主要使用精准率作为性能指标。

因为精准率高的话，则模型预测该股票要涨的可信度就高（很有可能赚钱！）。

比如现在需要训练一个模型来预测人是( $Positive $)否( \(Negtive\) )患有艾滋病，那么我们应该主要使用召回率作为性能指标。因为召回率太低的话，很有可能存在漏网之鱼（可能一个人本身患有艾滋病，但预测成了健康），这样就很可能导致病人错过了最佳的治疗时间，这是非常致命的。

标签：frac,预测,--,模型,衡量,性能指标,召回,sum,精准
来源： https://www.cnblogs.com/fjqqq/p/16096222.html