非易失性规划的原理与实现方法

　　常言道，计划不如变化快。计划的制定本身就建基于对未来一定时间范围内的环境条件假设，当计划制定后到执行完成的时间段内，若环境条件发生变化，那么计划也需要进行适当的调整才能满足实际要求。但计划的调整往往伴随着相应的代价，不仅仅是计划的重新制定所需的工作量，更大的代价来自于计划变更对执行工作的影响。例如提前备料、设备预调等准备工作；这是计划和控制的最大挑战之一；因此，计划的变更也极具研究价值。如何在环境条件发生变更导致原有计划无法继续执行时，快速定制一个最低成本的、切实可用的变更方案？本文我们主要考虑前后两个计划的延续性，来探讨如何在自动计划系统设计时，加入相应的建模方案，来实现计划变化的高延续性。一个变更后、且具有较高延续性的计划，我们叫做非易失性计划，“非易失性”一词来源于OptaPlanner用户手册-nonvolatile。

　　在生产计划、车辆调度、任务分配等场规划景中，均需要定时输出连续的计划；或对于已发布但未执行完成的计划，因环境条件发生变化，需要进行适度变更，也需输出一个修订计划。前后两次计划、或原始计划与修订计划之间必须存在一定的相关性，从而让实际的执行工作实现最大程度的延续性，此类规划称非易失性规划，即是指前后两次规划的差异具有可控性，通俗讲就是计划的变化需要在可控可接受范围内。其实现原理是在连续的规划过程中，在获取相对最优方案时，不能仅仅为了追求当前最优方案，还需要考虑计划的延续性；也可以理解为，计划的延续性也作为考察方案优劣的因素之一。

　　了解通过运筹规划来搜寻相对最优方案从而获得生产计划的朋友都知道，方案的优劣在规划模型中，反映为方案的目标函数值与理想极值的差异，差异越小方案越优。引擎(求解器)在规划运算过程中会对比各个方案的约束分数(目标函数值)差异，来逐步寻找更接近极值的方案。在可接受时间范围内得到的最优方案即为我们能获取的最终方案。若我们并未将前后两个计划的延续性作为目标函数的因子之一，则得到的相对最优方案，在延续性方面极可能会出现无法接受的结果，称为易失性计划。

　　例如：我们通过规划引擎自动生成生产计划，或物流车辆调度方案时(VRP方案)，首次生成的方案，当环境条件未产生变化时对实现的运输作业具有极高的指导价值，路径、时间最短，成本最低，新能源车辆充电时机最佳。但随着环境变化(例如路况变化、疫情导致地区封锁等情况发生)，旧的计划需要不断更新、适应新的环境变更，才能确保方案持续有效。再例如生产计划场景中，当一个具有一定周期的计划发布(或下达)后，完成在下一周期计划发布前的时间段内，计划发生意外情况，需要紧急修改计划中各个任务的优先级，或执行时间需要变更(紧急插单、生产设备计划外停机等情况)。均需要因应这些变更，重新定制一个新的可行的生产计划，而新的计划除了满足一些硬性约束和一些软性优化需求外，还需要考虑与原有工作的衔接。因为有可能存在一些任务需要提前备料、设备参数预设等需要一定时间且需提前完成的准备操作。若在新计划中被重新分配生产设备或原料，会导致浪费甚至新的计划不可行，例如：一个任务已完成备料，且已备好的原料不能回收，则只能在已备料的设备上生产(设备停机除外)。因此，在设计规划模型时，需要智能地防止此类“颠覆性”变化。

　　针对这种需要略显智能的场景要求，需要我们在设计约束分数时，进行稍微“人性化”的设计。OptaPlanner的用户手册关于持续计划一节中，有相关的指导说明。大家可以参与一下其用户手册中以下章节。

https://www.optaplanner.org/docs/optaplanner/latest/repeated-planning/repeated-planning.html#nonvolatileReplanning

　　通过上述用户手册章节可以理解到，所谓的人性化考虑，其设计过程也相当简单，只不过将“限制过度变化”也作为一种软件约束考虑，从而在一定程度上对引擎的“无序寻优”作出限制。可以参考官方示例中的Machine Reassignment, 该示例中每个Process(Planning Entity)有一个originalMachine对象，表示该Process当前分配到的设备，若新分配的Machine与该originalMachine对象不一致，即表示当前规划发生了设备切换，则使用相应的约束对该行为进行惩罚扣分。从而从一定程度上限制Process的随意切换问题。

　　详如下图，左边为原始方案，中间为变更后的易失性方案(产生的变更较大)，右则为非易失性方案(产生的变更相对小)。尽管从Cloud Balance示例的软约束分数评价(成本最低)来看，中间方案的成本更低200 + 350 = 550, 而右则的方案成本为200 + 400 = 600，但很明显右则方案在产生变更时，任务的移动更少，相对中间方案易失性更小。因此，在设计时添加了一个限制任务移动的约束，每移动一个任务的设备即扣罚100分，右则的方案评分(仅移动两个任务)更佳，加总后是扣分： 200 + 400 + 200 = 800，中间任务两种约束分数加总后扣分是950.即将移动任务也纳入评分后，右则的非易失性方案更佳。

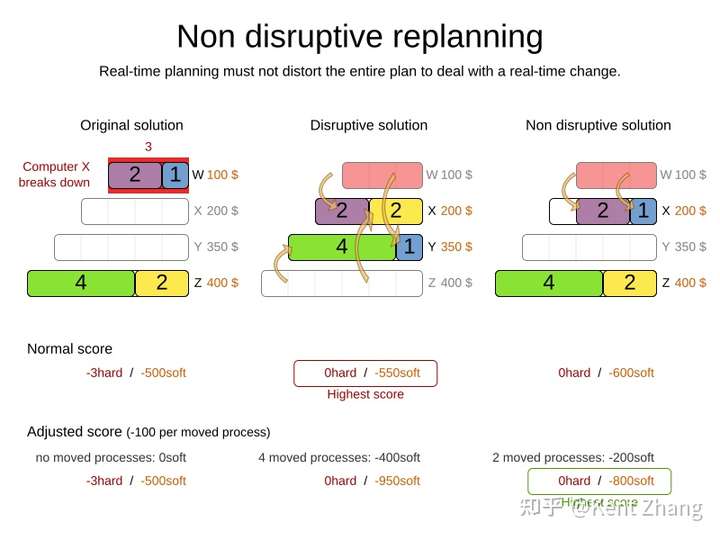
　　当然是否所有变更都是不好的呢？事实上具体情况需要视自己的业务场景而定。例如原始方案中所分配的资源已不可使用(机台发生意外停机，需要使用其它机台替代)，这种情况并不在限制变更的范围内(应该如何设计，大家可以自行思考一下)。另外一种情况相对更复杂一点，就是上述示例中的情况，需要对比变更的成本与收益，当收益高于成本时，即可挣脱变更限制。如果用户手册中的一句话即可概括：the gain of changing a plan must be higher than the disruption it causes。

本系列文章在公众号不定时连载，请关注公众号（搜“让APS成为可能”或扫以下QR Code）及时接收,二维码：

如需了解更多关于OptaPlanner的应用，请发电邮致：kentbill@gmail.com
或到讨论组发表你的意见：https://groups.google.com/forum/#!forum/optaplanner-cn
若有需要可添加本人微信（13631823503）或QQ(12977379)实时沟通，但因本人日常工作繁忙，通过微信,QQ等工具可能无法深入沟通，较复杂的问题，建议以邮件或讨论组方式提出。(讨论组属于google邮件列表，国内网络可能较难访问，需自行解决)

标签：方案,需要,延续性,非易,计划,失性,原理,变更
来源： https://www.cnblogs.com/kentzhang/p/15962907.html