Lab10 of CS61A of UCB

Q2: Over or Under

Define a procedure over-or-under which takes in a number num1 and a number num2 and returns the following:

• -1 if num1 is less than num2
• 0 if num1 is equal to num2
• 1 if num1 is greater than num2

Challenge: Implement this in 2 different ways using if and cond!

(define (over-or-under num1 num2)
  'YOUR-CODE-HERE
)

代码其实本身不难, 主要是适应 scheme 语言的写法, 条件分支有两种写法:

1. (if <predicate> <consequent> <alternative>)
2. (cond (<condition> <consequent>) ...)

(define (over-or-under num1 num2) 
    (if (< num1 num2) 
            (print -1))
    (if (= num1 num2)
            (print 0))
    (if (> num1 num2)
            (print 1))
)

(define (over-or-under num1 num2)
  (cond ( (< num1 num2) (print -1) )
        ( (= num1 num2) (print 0)  )
        ( (> num1 num2) (print 1)  ))
)

Q3: Make Adder

Write the procedure make-adder which takes in an initial number, num, and then returns a procedure. This returned procedure takes in a number inc and returns the result of num + inc.

Hint: To return a procedure, you can either return a lambda expression or define another nested procedure. Remember that Scheme will automatically return the last clause in your procedure.

You can find documentation on the syntax of lambda expressions in the 61A scheme specification!

实现高阶函数的功能, 依旧是锻炼 scheme 语言的掌握程度的. 题目都是之前课上讲过的. 这里我用匿名函数来实现

(define (make-adder num)
  (lambda (inc) (+ num inc))
)

Q4: Compose

Write the procedure composed, which takes in procedures f and g and outputs a new procedure. This new procedure takes in a number x and outputs the result of calling f on g of x.

用 scheme 语言实现符合数学中的复合函数, 也就是高阶函数. 这里同样可以用 lambda 函数

(define (composed f g)
  (lambda (x) (f (g x) ) )
)

Q5: Make a List

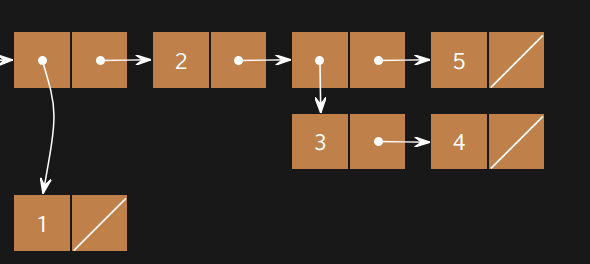
In this problem you will create the list with the following box-and-pointer diagram:

Challenge: try to create this list in multiple ways, and using multiple list constructors!要求

题目要求我们按照给定的链表结构来生成对应的链表. 主要考察的是对 scheme 语言中 list 的掌握. 可以有多种实现方式

1. cons 的方式, 这个方式很容易眼花, 最好是写完之后在这里 验证一下. 这里我真的写得头有点晕

   标签：num1,num2,list,CS61A,item,lst,UCB,Lab10,procedure
   来源： https://www.cnblogs.com/MartinLwx/p/15942040.html