3.1 内容概要

• PPT
  • 控制系统零、极点的概念
  • 控制系统的暂态响应
  • 线性时不变系统的概念
  • 劳斯-赫尔维兹稳定性判据
  • 稳态误差
• 自己总结
  • 从高阶系统可以拆分为叠加在一起的低阶系统这一想法出发，本章首先研究的，是作为系统基本组成部分的一阶系统和二阶系统。
  • 虽然这个想法是好的，但在实际操作中做部分因式分解还是太麻烦（我感觉），所以接着又在不做拆分的条件下，讨论了极点位置对高阶系统的特性的影响。
  • 然而高阶系统的极点没有解析解，经常不容易全部找出来，所以接着又讨论了几个能在不求出全部极点的条件下，判断系统是否稳定的方法。
  • 最后在系统稳定的条件下，讨论了系统的稳态误差。

3.2 暂态响应分析

暂态响应：课上没有说明，自己找了找发现课上表达的意思和其他地方定义的意思不大一样，不过简单理解应该就是指：系统从时间零点到稳定之前这一段时间内的零状态（为了便于比较不同系统而默认是零状态）时域响应。

3.2.1 零点与极点

定义

对于传递函数\(G(s)\)，可以通过部分因式分解将其化为以下形式

\[\begin{aligned} G(s)=& \frac{c_{1,1}}{\left(s-p_{1}\right)^{n_{1}}}+\frac{c_{1,2}}{\left(s-p_{1}\right)^{n_{1}-1}}+\cdots+\frac{c_{1, n_{1}}}{s-p_{1}} \\ &+\frac{c_{2,1}}{\left(s-p_{2}\right)^{n_{2}}}+\frac{c_{2,2}}{\left(s-p_{2}\right)^{n_{2}-1}}+\cdots+\frac{c_{2, n_{2}}}{s-p_{2}}+\cdots \\ &+\frac{c_{m, 1}}{\left(s-p_{m}\right)^{n_{m}}}+\frac{c_{m, 2}}{\left(s-p_{m}\right)^{n_{m}-1}}+\cdots+\frac{c_{m, n_{m}}}{s-p_{m}}+b_{n} \end{aligned} \]

• 极点\(p_i\)满足\(\lim\limits_{s\to p_i}|G(s)|=\infty\)
• 零点\(z_i\)满足\(\lim\limits_{s\to z_i}|G(s)|=0\)

---

• 这样的定义可以把无穷远处的零点也考虑在内。

• 对于分子分母不可再约分的传递函数，由定义易知极点是分母的根，零点是分字的根。

• 对于实系数的传递函数来说，一个复数零点/极点的共轭复数一定还是其零点/极点。

  这个性质需要以下结论：系数为实数的一元n次方程的复数解总是共轭地成对出现。

  证明：设\(x_0\)为一元n次方程\(\sum\limits_{i=0}^na_ix^i=0,a\in\mathbb R\)的根，对等式两边取共轭有

  \[\sum\limits_{i=0}^na_ix_0^i=0\\ \sum\limits_{i=0}^n\overline{a_ix_0^i}=0\\ \sum\limits_{i=0}^na_i\overline x_0^i=0 \]

  即有\(x_0\)的共轭仍是该方程的根。

  • 部分因式的系数由留数定理确定：\(c_{i,j}=\frac{1}{(j-1)!}\lim_\limits{s\to p_i}\frac{\mathrm{d}^{j-1}}{\mathrm{d}s^{j-1}}(s-p_i)^jG(s)\)。故共轭零点/极点的系数也是共轭的。

构成控制系统的基本元素——一阶系统和二阶系统

上述系统拆分成的部分因式可以根据极点是哪一种根而分为三类：非重根的实根、非重根的复数根和重根。

• 非重根的实根对应的部分因式表示了一个一阶系统
• 非重根的复数根对应的两个共轭的部分因式之和表示了一个二阶系统
• 重根对应的部分因式可以看作是前边二者在复频域的导数。

对于后两种情况，具体算一下来说明：用\(p_i=\sigma_i+j\omega_i\)和\(p_{i+1}=\overline p_i\)表示一对共轭极点，合并二者的部分因式得到：

\[\frac{c_{i,j}}{(s-p_i)^{n_i-j+1}}+\frac{\overline c_{i,j}}{(s-\overline p_i)^{n_i-j+1}} =\frac{c_{i,j}(s-\overline p_i)^{n_i-j+1}+\overline c_{i,j}(s-p_i)^{n_i-j+1}}{[(s-\sigma_i)^2+\omega_i^2]^{n_i-j+1}} \]

• 如果\(p_i\)、\(p_{i+1}\)是非重根的复数根，即\(j=n_i\)的情况，有

  \[\left. [\frac{c_{i,j}}{(s-p_i)^{n_i-j+1}}+\frac{\overline c_{i,j}}{(s-\overline p_i)^{n_i-j+1}}] \right|_{j=n_i} =\frac{s(c_{i,n_i}+\overline c_{i,n_i})-(c_{i,n_i}\overline p_i+\overline c_{i,n_i}p_i)}{(s-\sigma_i)^2+\omega_i^2} \]

  这表示了一个二阶系统。

  系统的阶次：传递函数分母的最高次。

• 如果\(p_i\)、\(p_{i+1}\)是重根的复数根，即\(j<n_i\)的情况，有

  \[\begin{aligned} &\frac{c_{i,j}}{(s-p_i)^{n_i-j+1}}+\frac{\overline c_{i,j}}{(s-\overline p_i)^{n_i-j+1}}\\ =&-\frac{1}{n_i-j}\frac{\mathrm{d}}{\mathrm{d}s}[\frac{c_{i,j}}{(s-p_i)^{n_i-j}}+\frac{\overline c_{i,j}}{(s-\overline p_i)^{n_i-j}}] \end{aligned} \]

  对方括号中的内容重复以上操作，可以使\((s-p_i)\)的次数逐渐降低至1，所以其表示的系统的传递函数，是一个二阶系统的传递函数在复频域的\(n_i-j\)阶导数。

由拉普拉斯变换的性质又有

\[\mathcal L[tf(t)]=-\frac{\mathrm d}{\mathrm d s}\tilde f(s) \]

所以如果了解了一阶系统\(\frac{1}{s-p_i}\)和二阶系统\(\frac{\alpha_i s+\beta_i}{(s-\sigma_i)^2+\omega_i^2}\)的时域响应，就可以方便地得到任意部分因式所表示的系统的时域响应，进而通过线性叠加就可以得到任意系统的时域响应。因此，称一阶系统和二阶系统是构成控制系统的基本元素

3.2.2 一阶系统的暂态响应

单位负反馈形式的一阶系统

标准一阶系统的微分方程和传递函数如下

\[T\dot y(t)+y(t)=r(t)\\ \dot y(t)=\frac{1}{T}[r(t)-y(t)]\\ \Rightarrow \frac{\tilde y(s)}{\tilde r(s)}=\frac{1}{Ts+1} \]

• \(T\)称为时间常数。

对应的系统框图如下

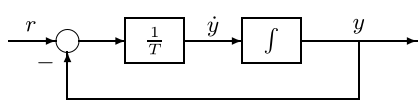
单位冲激响应（Unit-Impulse Response）

\[\tilde y(s)=\frac{1}{Ts+1}\\ \Rightarrow y(t)=\frac{1}{T}e^{-\frac{t}{T}},\ t\ge0 \]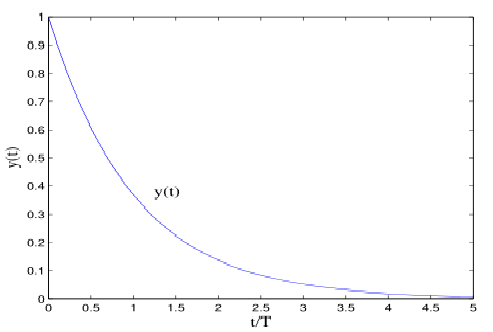

注意横坐标的单位是\(T\)，下同。

单位阶跃响应（Unit-Step Response）

输入为阶跃函数\(r(t)=u_{-1}(t)\)，有

\[\tilde y(s)=\frac{1}{Ts+1}\cdot \frac{1}{s}=\frac{1}{s}-\frac{1}{s+1/T}\\ \Rightarrow y(t)=1-e^{-\frac{t}{T}},\ t\ge0 \]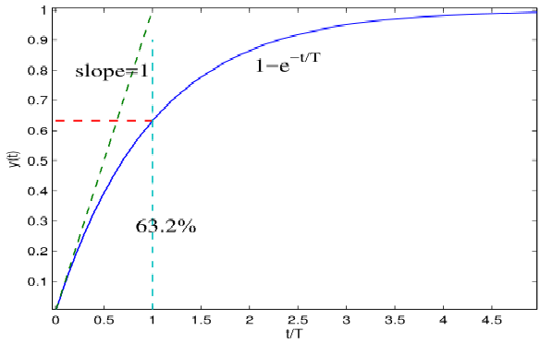

• \(y(T)\approx0.632\)，\(y(4T)\approx0.9817\)

• \(\log|y(t)-y(\infty)|\)曲线可以用于辨识一阶系统，因为只有一阶系统在该曲线中是一条直线：

  \[\log|y(t)-y(\infty)|=-\frac{t}{T} \]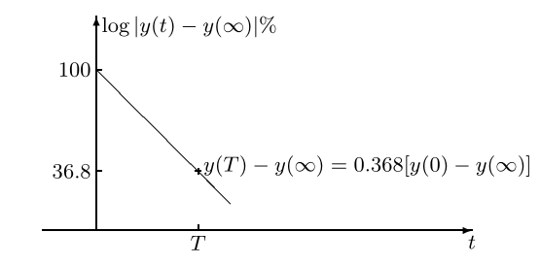

  

单位斜坡响应（Unit-Ramp Response）

\[\tilde y(s)=\frac{1}{Ts+1}\cdot \frac{1}{s^2}=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+1/T}\\ \Rightarrow y(t)=t-T+Te^{-\frac{t}{T}},\ t\ge0 \]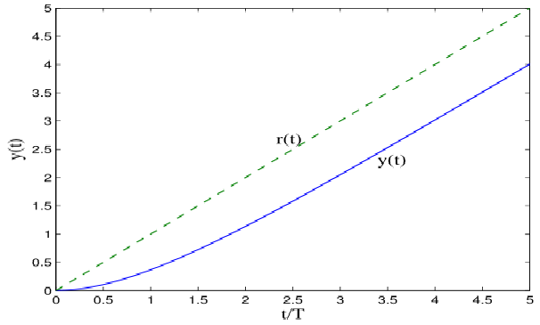

• 可以定义误差信号
  \[e(t)=r(t)-y(t)=T(1-e^{-\frac{t}{T}}) \]

---

可以发现单位冲激响应是单位阶跃响应的导数，单位阶跃响应是单位斜坡响应的导数，这个规律可以推广到其它LTI（Linear Time-Invariant）系统。

3.2.3 二阶系统的暂态响应

标准二阶系统

定义如下

\[\frac{\tilde{y}(s)}{\tilde{r}(s)}=\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}=\frac{\frac{\omega_{n}^{2}}{s\left(s+2 \zeta \omega_{n}\right)}}{1+\frac{\omega_{n}^{2}}{s\left(s+2 \zeta \omega_{n}\right)}} \]

• 其中\(\omega_n\)称为无阻尼固有频率（undamped natural frequency），\(\zeta\)称为阻尼比（damping ratio）。

• 对于非标准二阶系统（分子上带\(s\)的），响应可能很不一样，可以化成多个标准系统或标准系统的导数的叠加来进行分析。

• 单位反馈形式的系统框图如下

  

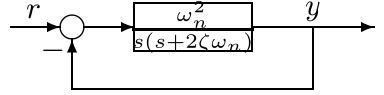
单位阶跃响应

由单位阶跃响应，有\(r(s)=\frac{1}{s}\)。

欠阻尼状态

有\(0<\zeta<1\)。定义阻尼固有频率（ damped natural frequency）\(\omega_d\triangleq\omega_n\sqrt{1-\zeta^2}\)，则传递函数可以改写为

\[\frac{\tilde{y}(s)}{\tilde{r}(s)}=\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\zeta^2\omega_n^2+\omega_{d}^{2}}=\frac{\omega_{n}^{2}}{(s+\zeta\omega_n)^{2}+\omega_{d}^{2}} \]

做部分因式分解

\[\tilde y(s)=\frac{\omega_{n}^{2}}{s[(s+\zeta\omega_n)^{2}+\omega_{d}^{2}]}=\frac{c_1}{s}+\frac{c_2}{s+\zeta\omega_n+j\omega_d}+\frac{\overline c_2}{s+\zeta\omega_n-j\omega_d} \]

由留数定理

\[\begin{aligned} c_{1} &=\lim _{s \rightarrow 0} s \cdot \tilde{y}(s)=\frac{\omega_{n}^{2}}{\omega_{n}^{2}}=1 \\ c_{2} &=\lim _{s \rightarrow-\left(\zeta \omega_{n}+j \omega_{d}\right)}\left(s+\zeta \omega_{n}+j \omega_{d}\right) \tilde{y}(s)\\ &=\left.\frac{\omega_{n}^{2}}{s\left(s+\zeta \omega_{n}-j \omega_{d}\right)}\right|_{s=-\left(\zeta \omega_{n}+j \omega_{d}\right)} \\ &=\frac{\omega_{n}^{2}}{2 j \omega_{d}\left(\zeta \omega_{n}+j \omega_{d}\right)}\\ &=-\frac{\omega_n^2}{2\omega_d(\zeta^2\omega_n^2+\omega_d^2)}(\omega_d+j\zeta\omega_n) \end{aligned} \]

带入化简得（这一步具体算起来比较麻烦）

\[\begin{aligned} &\frac{c_2}{s+\zeta\omega_n+j\omega_d}+\frac{\overline c_2}{s+\zeta\omega_n-j\omega_d}\\ =&-\frac{s+2\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}\\ =&-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}-\frac{\zeta\omega_n}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2} \end{aligned} \]

于是可以进一步化简复频域响应

\[\tilde y(s)=\frac{1}{s}-\frac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2}-\frac{\zeta\omega_n}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2} \]

定义\(\cos\varphi\triangleq\zeta\)，则时域响应为

\[\begin{aligned} y(t)=&1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}[\sqrt{1-\zeta^2}\cos(\omega_dt)+\zeta\sin(\omega_dt)]\\ =&1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}\sin(\omega_dt+\varphi)\\ =&1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}\sin(\sqrt{1-\zeta^2}\omega_nt+\varphi),\ t\ge 0\\ \end{aligned} \]

具体求解时域响应不是重点，主要是要熟悉\(\zeta\)对标准二阶系统暂态响应、极点分布的影响，下同。

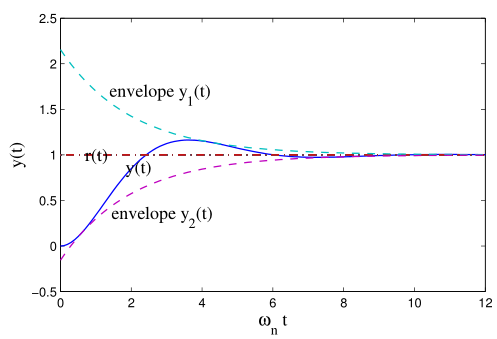
• 暂态响应的时域图象

  • 注意横坐标单位是\(\omega_n t\)，下同。
  • 波形是被限制在两个指数衰减函数间的减幅振荡

• \(\zeta\)对欠阻尼状态二阶系统暂态响应的影响

  

• \(\omega_n\)、\(\omega_d\)、\(\zeta\)和极点在复平面上的关系

  

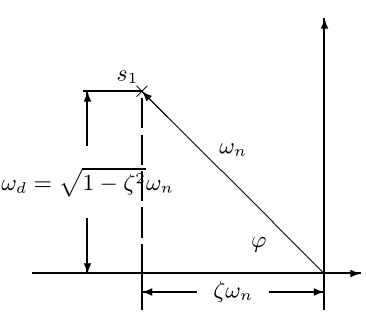
临界阻尼状态

有\(\zeta=1\)。

\[\tilde y(s)=\frac{\omega_n^2}{s(s+\omega_n)^2}=\frac{1}{s}+\frac{-\omega_n}{(s+\omega_n)^2}+\frac{-1}{s+\omega_n}\\ \Rightarrow y(t)=1-\omega_nte^{-\omega_nt}-e^{-\omega_nt}=1-e^{-\omega_nt}(\omega_nt+1) \]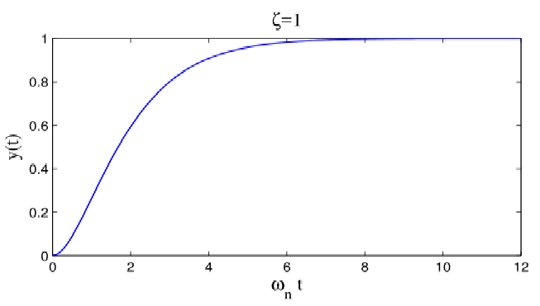

• 看着像一阶系统的阶跃相应，不过此处在零时刻输出的增长速度为0

过阻尼状态

有\(\zeta>1\)。直接求极点+留数定理算就完啦，结果表示比较复杂，可以用极点

\[\left\{ \begin{aligned} s_1&=-\zeta\omega_n-\omega_n\sqrt{\zeta^2-1}\\ s_2&=-\zeta\omega_n+\omega_n\sqrt{\zeta^2-1} \end{aligned} \right. \]

表示成简化一些的如下形式

\[\begin{aligned} y(t)=&1+\frac{1}{2\sqrt{\zeta^2-1}}(\frac{e^{-(\zeta+\sqrt{\zeta^2-1})\omega_nt}}{\zeta+\sqrt{\zeta^2-1}}+\frac{e^{-(\zeta-\sqrt{\zeta^2-1})\omega_nt}}{\zeta-\sqrt{\zeta^2-1}})\\ =&1+\frac{\omega_n}{2\sqrt{\zeta^2-1}}(\frac{e^{s_1t}}{-s_1}+\frac{e^{s_2t}}{s_2})\\ \end{aligned} \]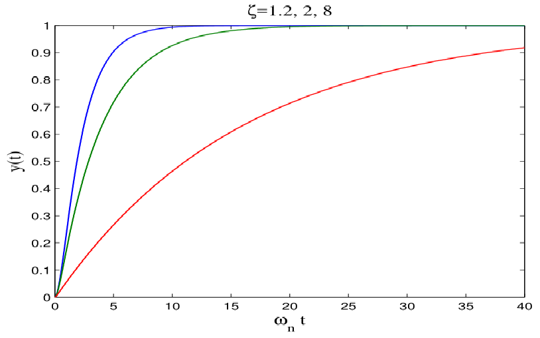

• 当\(\zeta\)较大时，\(e^{s_1t}\)衰减相比\(e^{s_2t}\)将快得多，导致系统的暂态响应主要由\(e^{s_2t}\)影响，于是给像\(s_2\)这样的极点取了个名字，叫主导极点（本章后面小节还有相关内容）。

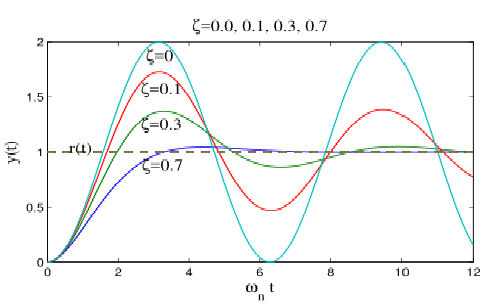
\(\zeta\)对标准二阶系统的影响

• 观察上面三种情况的结果，当把\(\omega_nt\)视作一个整体变量后，系统的时域响应只与\(\zeta\)有关。这也即是说，如果两个标准的二阶系统的\(\zeta\)相同，通过调节座标轴的比例可以使它们的时域响应曲线看起来一模一样。
• \(\zeta<1\)的欠阻尼系统相比其他二者能更快地靠近到目标值，但是存在振荡；\(\zeta=0\)的临界阻尼系统是无震荡的标准二阶系统中最快靠近目标值的。

二阶系统的时域指标

因为阶跃输入易于产生，且在数学上有了阶跃响应就可以推知任意输入的响应，所以经常用阶跃响应中的一些指标来描述系统的特性。本节即计算欠阻尼二阶系统单位阶跃响应中的一些常用指标。

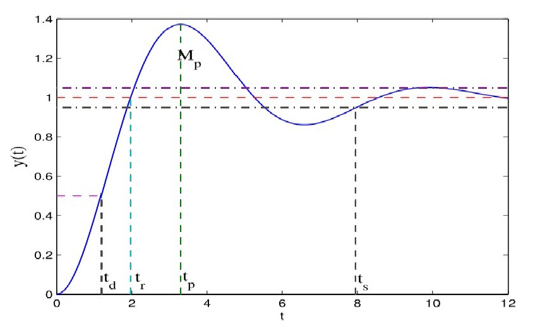
• 延迟时间\(t_d\)（delay time）：第一次到达终值的一半的时刻。

• 上升时间\(t_r\)（rise time）：从终值的0%、5%、或10%上升到终值的90%、95%、或100%所需要的时间，对处于不同状态的二阶系统会取不同的范围，此处取0%~100%。

  令\(y(t_r)=1\)，有

  \[\begin{aligned} 1-\frac{e^{-\zeta\omega_nt_r}}{\sqrt{1-\zeta^2}}\sin(\omega_dt_r+\varphi)&=1\\ \sin(\omega_dt_r+\varphi)&=0\\ \Rightarrow \omega_nt_r=\frac{\pi-\arccos\zeta}{\sqrt{1-\zeta^2}}=\frac{\pi-\varphi}{\sin\varphi} \end{aligned} \]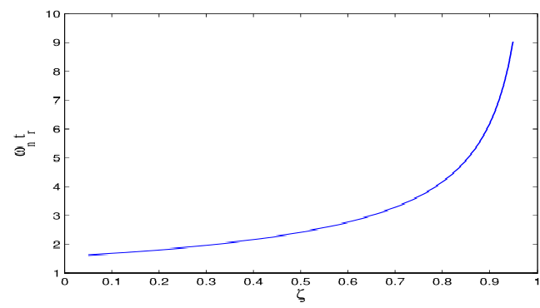

  

• 峰值时间\(t_p\)（peak time）：到达超调的第一个顶峰的时刻，这个顶峰一般对应最大超调量。

  时域导数为0时达到峰值，有

  \[\left.\frac{\mathrm d}{\mathrm d t}[1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}\sin(\omega_dt+\varphi)]\right|_{t=t_p}=\frac{\omega_ne^{-\zeta\omega_nt_p}}{\sqrt{1-\zeta^2}}\sin(\omega_dt_p)=0\\ \Rightarrow \omega_nt=\omega_nt_p=\frac{\pi}{\sqrt{1-\zeta^2}}=\frac{\pi}{\sin\varphi} \]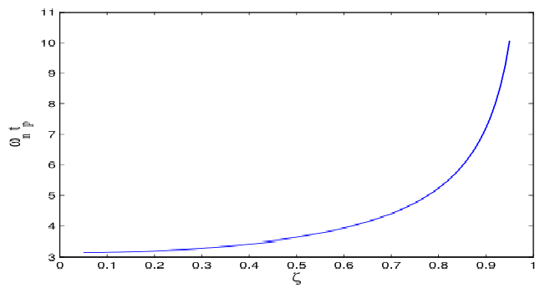

  

• 最大超调量\(M_p\)（或者是\(\sigma\%\)）（maximum overshoot）：单位化的最大正向误差。

  如果第一个峰值对应最大超调量，则有\(M_p=\frac{y(t_p)-y(\infty)}{y(\infty)}\)。带入峰值时间计算可得

  \[M_p=[y(t_p)-1]\times100\%=e^{-\frac{\zeta}{\sqrt{1-\zeta^2}}\pi}\times100\%=e^{-\pi\cot\varphi}\times100\% \]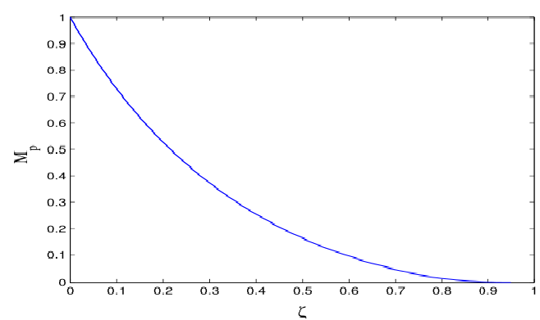

  

• 调节时间\(t_s\)（settling time）：该时刻之后，误差只会在一定范围（一般取2%~5%）内浮动。

  没有解析公式且变化不连续，工程上使用经验公式

  \[\omega_nt_s\approx\frac{4}{\zeta}\quad for\ 2\%\ criterion\\ \omega_nt_s\approx\frac{3}{\zeta}\quad for\ 5\%\ criterion \]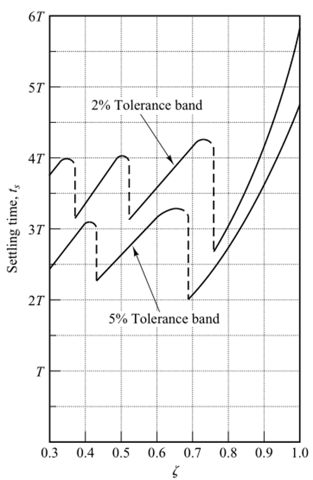

  

伺服系统的速度反馈

引入速度反馈可能改善系统性能（改变二阶系统的\(\zeta\)），这一节介绍了一个例子。一个带有速度反馈的伺服系统的简化系统框图如下

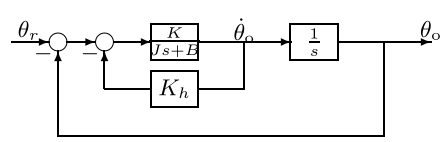
消去内环得到

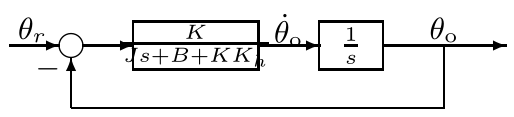
求其传递函数如下

\[\frac{\tilde\theta(s)}{\tilde\theta_r(s)}=\frac{\frac{K}{(Js+B+KK_h)s}}{1+\frac{K}{(Js+B+KK_h)s}}=\frac{K/J}{s^2+(B+KK_h)/J\cdot s+K/J} \]

于是得到

\[\left\{ \begin{aligned} \zeta=&\frac{B+KK_h}{2\sqrt{KJ}}\\ \omega_n=&\sqrt{K/J} \end{aligned} \right. \]

于是，在引入速度反馈后，通过调节\(K_h\)可以在不影响\(\omega_n\)的条件下改变\(\zeta\)（引入速度反馈之前调节\(\zeta\)会同时影响\(\omega_n\)），进而使系统的性能达到需要理想状态。不过需要注意的是，因为噪声一般都是高频的，引入速度反馈可能会放大噪声。

标签：frac,暂态,响应分析,nt,系统,sqrt,zeta,自控,omega
来源： https://www.cnblogs.com/harold-lu/p/15720566.html