傅里叶变换

时域和频域

音乐类比：波形图是时域，乐谱（音符）是频域

单个音符是一个正弦波，不同振幅不同相位的正弦波叠加，可以构成任意波形

也就是说，任何周期函数都可以由正弦波叠加而成

傅里叶级数的频谱

我们用一系列正弦波叠加成矩形波

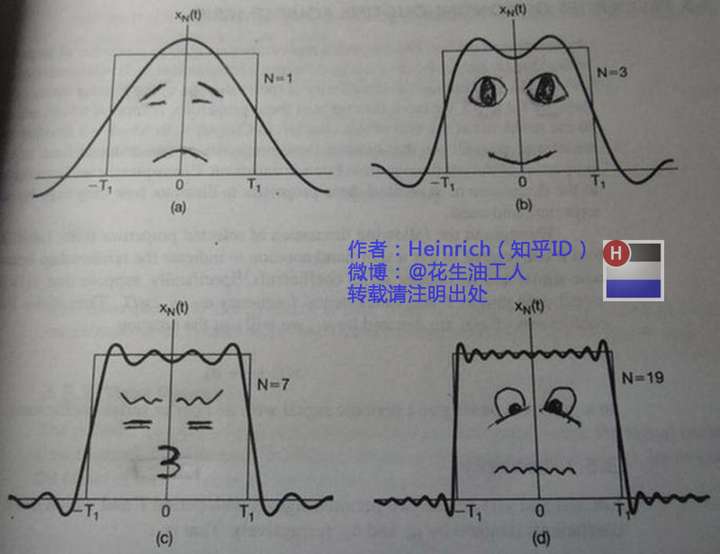
称不同频率的正弦波为频率分量

特别地，0频率（直线）被称为直流分量，它只造成整体上下平移

它的频域是这样的

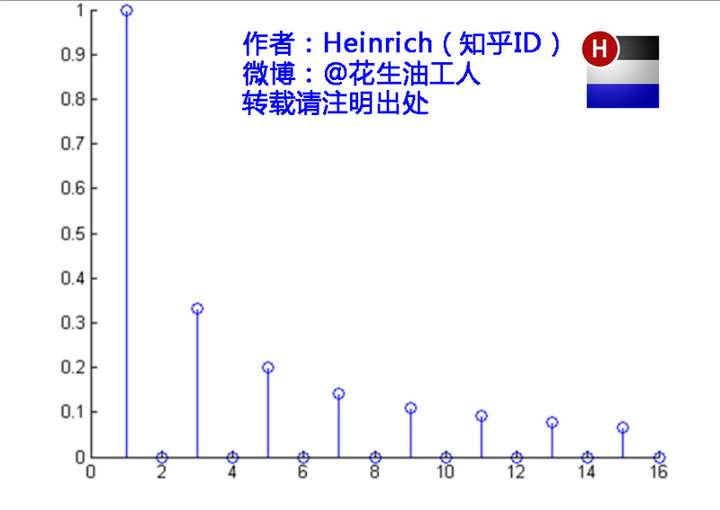
为什么？

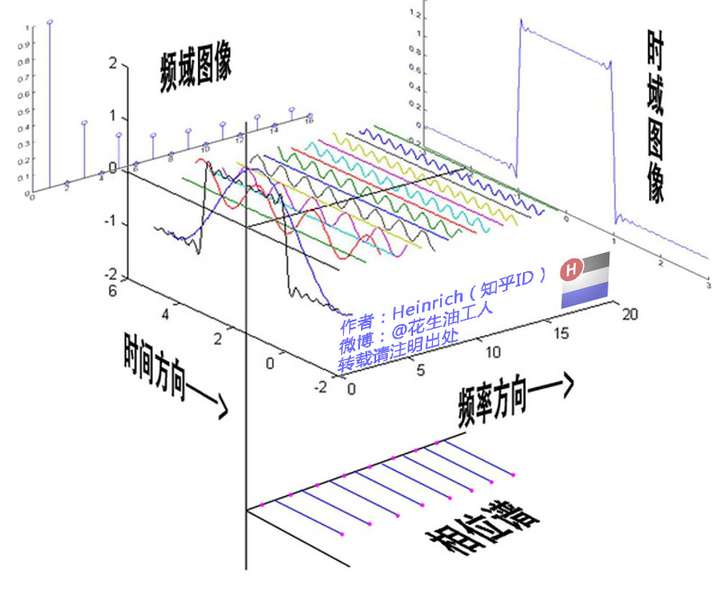
从三维空间看这些正弦波，如下：

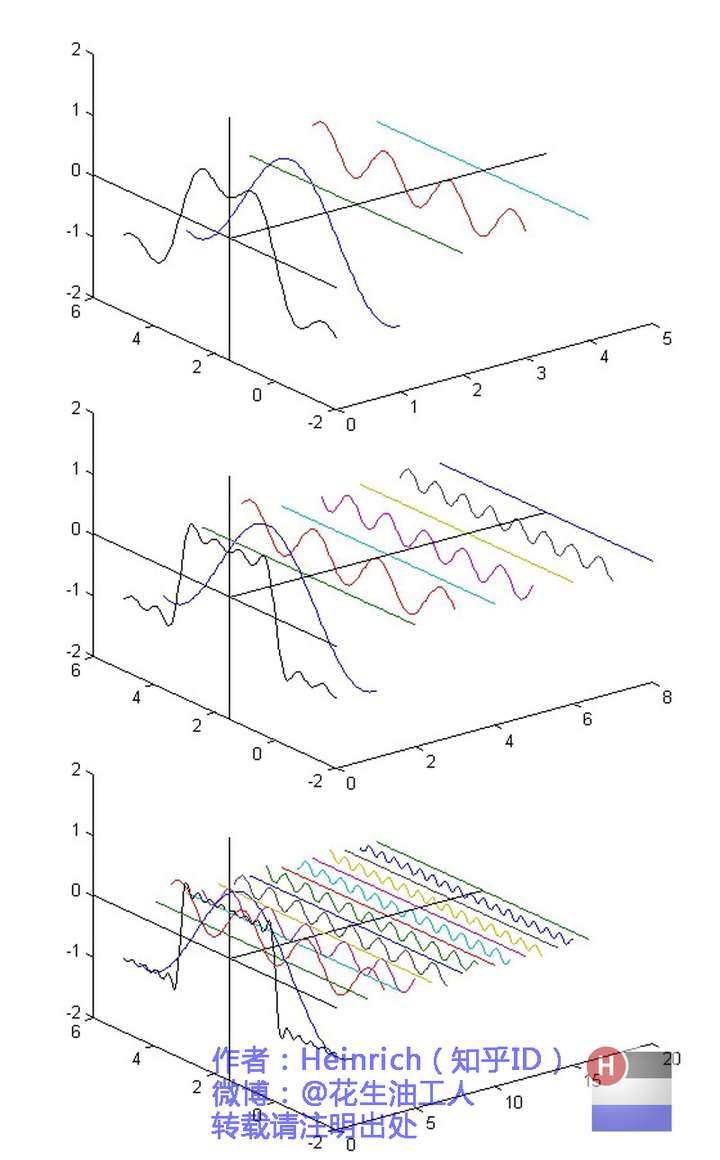
时域就是正面看，频域就是侧面看

傅里叶变换就是时域和频域之间的转换

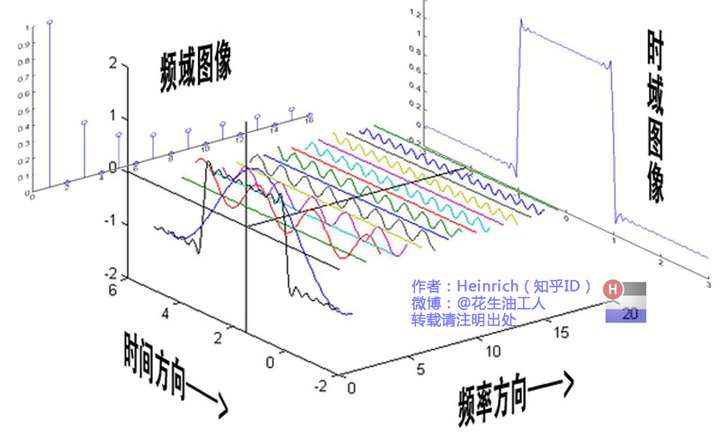
傅里叶级数的相位谱

很多在时域不好做的操作，在频域可以轻松做到

确定一条正弦波需要知道振幅、频率和相位，从侧面看保留了振幅（y轴）和频率（x轴）信息

相位信息从哪来？

我们将离频率轴最近的波峰标记一个红点，再投影到下平面上，就得到了相位谱

傅里叶变换

终于到了傅里叶变换部分

我们要通过它，将时域的连续信号转化为频域的连续信号

区别于傅里叶级数，它将时域的连续信号转化成频域的离散信号

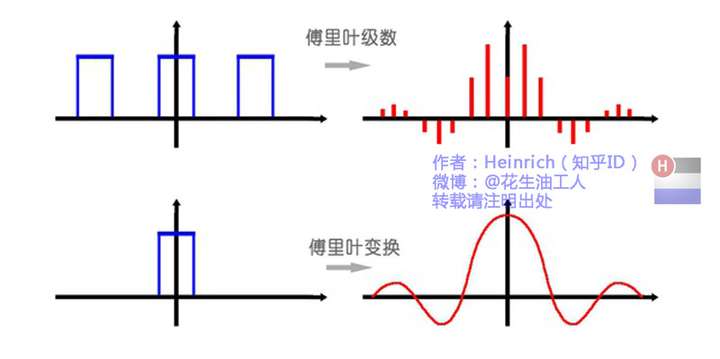
离散信号足够密集，就类似连续信号了

也就从求和符号变成积分符号了

欧拉公式

\[e^{ix}=\cos x+i\sin x \]

乘以\(i\)可以看成旋转90°（参考三蓝一棕）

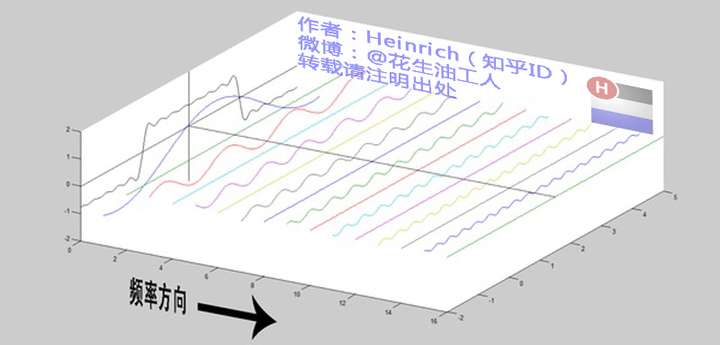
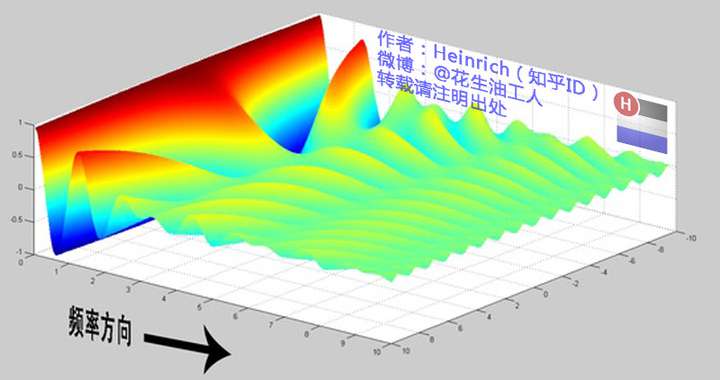
从复平面法向量方向拉一条时间轴，用\(t\)替换\(x\)，那么\(e^{it}\)可以看成一条螺旋线

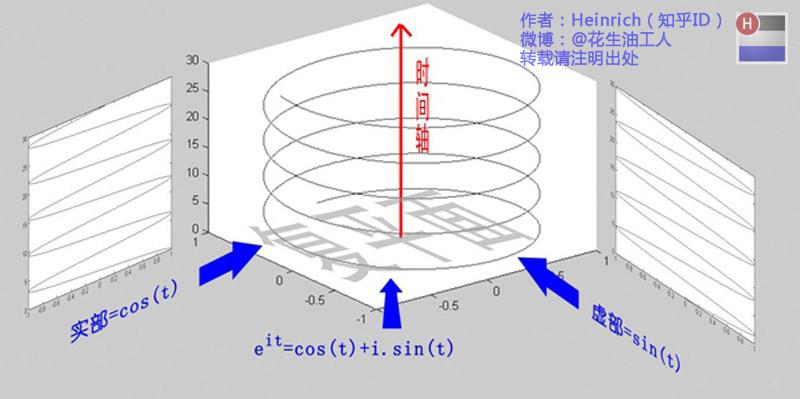
指数形式的傅里叶变换

由上图，正弦波的叠加，可以看成螺旋线的叠加在实数空间的投影

振幅——旋转半径

频率——旋转周期

相位——位置

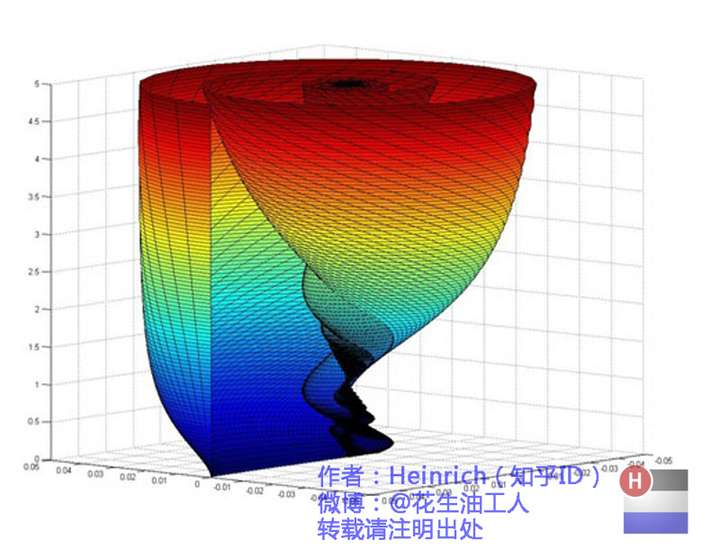
最终结果是这样的

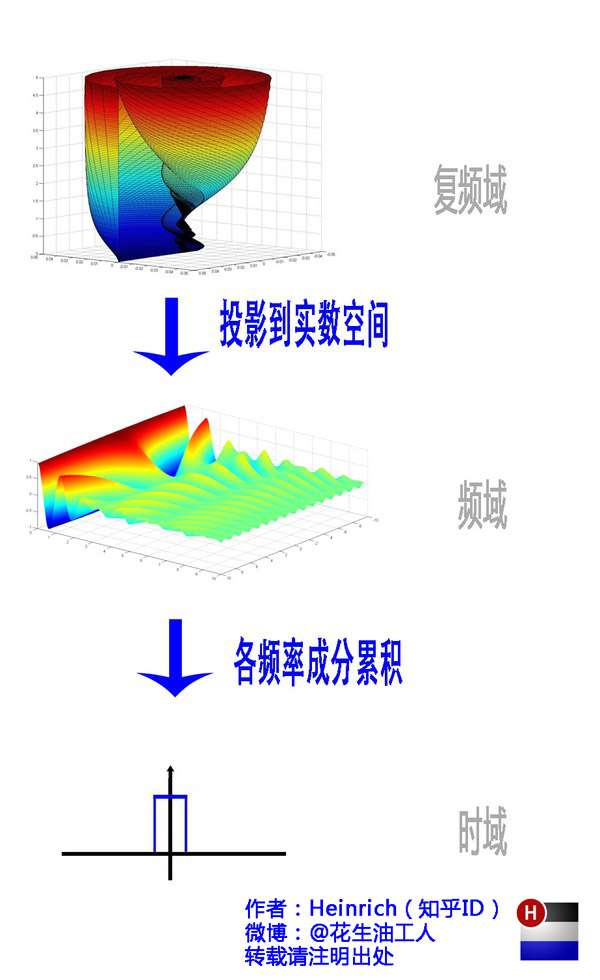
一维公式

时域信号f(t)的傅里叶变换为

\[F(\omega)=\mathscr{F}[f(t)]=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt \]

理解：对每个t，求\(f(t)\)和\(e^{-j\omega t}\)的内积，再求和，即\(f(t)\)在正弦波\(e^{-j\omega t}\)上的投影​

反变换为

\[f(t)=\mathscr{F}^{-1}[F(\omega)]=\dfrac{1}{2\pi}\int_{-\infty}^{\infty}F(j\omega)e^{-j\omega t}d\omega \]

二维公式

将一个图像分解成复平面波之和

\[F(u,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-j2\pi(ux+vy)}dxdy \]

同样可以理解为：图像与不同频率不同方向的复平面波内积求和，即投影的过程

K空间

K空间即二维频率域

确定一个二维正弦平面波需要四个参数：振幅、频率、相位和方向向量

用复数存储幅振幅和相位，用二维向量表示频率和方向

（向量的方向为正弦波方向，向量的模长为频率，向量终点存复数）

理解一下，越靠近中心原点，模长越小，频率越小，对应低频信息，提供主体信息

反之，越远离中心，模长越大，频率越大，对应高频信息，提供细节信息

更好地理解了SOD里的结论：

high-level features help locate the salient objects roughly, low-level features help refine boundaries.

这些向量放到二维平面中，就是K-SPACE了

K空间的每个复数代表了复平面波在原图像中占有多少成分，复系数乘以平面波相加就能得到原图像

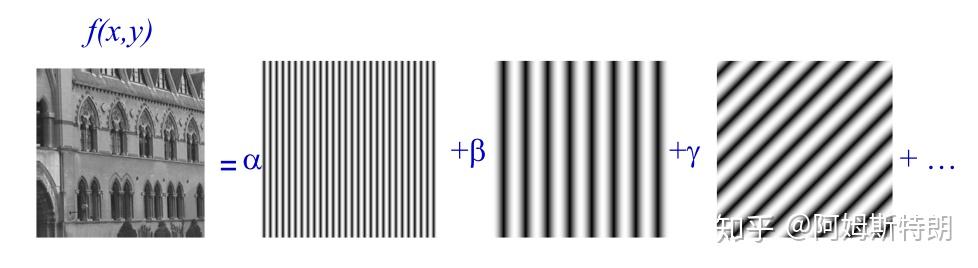
平面波是基，K空间的数是系数，叠加就是原信息

K空间里的相位保留位置信息，幅度保留强度信息

图像旋转，K空间也旋转

Convolution Theorem

空间卷积=频域乘积

类似FFT，要对两个图像卷积，先分别FT，再相乘，再IFT即可

Sampling Theorem

如果f(x,y)的傅里叶变换对频率大于\(u_b\)和\(v_b\)的都为0

那么只要采样距离\(w\le\dfrac{1}{2u_b}\),\(h\le\dfrac{1}{2v_b}\)​，原图像就可以被完全恢复

标签：infty,变换,omega,正弦波,笔记,频域,频率,傅里叶
来源： https://www.cnblogs.com/ghostcai/p/15704702.html