Rate–distortion theory and human perception

Publication Information

Author: Chris R. Sims (Citations: 1216)

Publisher: Cognition (Impact Factor: 3.650, ranking: 17 out of 90)

Abstract

Scene: The fundamental goal of perception is to aid in the achievement of behavioral objectives. This requires extracting and communicating useful information from noisy and uncertain sensory signals. At the same time, given the complexity of sensory information and the limitations of biological information processing, it is necessary that some information must be lost or discarded in the act of perception. Under these circumstances, what constitutes an ‘optimal’ perceptual system?

Contributions: This paper describes the mathematical framework of rate–distortion theory as the optimal solution to the problem of minimizing the costs of perceptual error subject to strong constraints on the ability to communicate or transmit information.

• Models developed in this framework are capable of producing quantitatively precise explanations for human perceptual performance, while yielding new insights regarding the nature and goals of perception.
• This paper demonstrates the application of rate–distortion theory to two benchmark domains where capacity limits are especially salient in human perception: discrete categorization of stimuli (also known as absolute identification) and visual working memory.
• A software package written for the R statistical programming language is described that aids in the development of models based on rate–distortion theory.

Introduction

Rate–distortion theory shares much in common with the probabilistic inference approach to perception (Kersten, Mamassian, &Yuille, 2004; Knill & Richards, 1996) and in particular Bayesian decision theory (Körding, 2007; Maloney & Mamassian, 2009).Hence, rate–distortion theory has much to say about how biological organisms should behave in a particular environment, in keeping with ideal observer (Geisler, 2011) or rational analysis(Anderson, 1990) approaches to understanding human cognition.

Rate-distortion theory is then applied to two domains: absolute identification (the assignment of perceptual stimuli to ordinal categories) and perceptual working memory. In each case, rate–distortion theory contributes something fundamentally new to the understanding of human perception.

Rate-distortion Theory

It is often difficult to directly compute the channel capacity, as this requires complete and accurate knowledge of the channel distribution \(P(y|x)\). However, measuring performance or accuracy is often much easier. Having a rate–distortion curve allows one to directly map between these two quantities and infer a lower bound on channel capacity.

Absolute identification

Introduction

An absolute identification experiment consists of repeatedly presenting the subject with a randomly chosen stimulus, and asking the subject to respond with his or her best guess regarding the ordinal identity of the stimulus.

Result

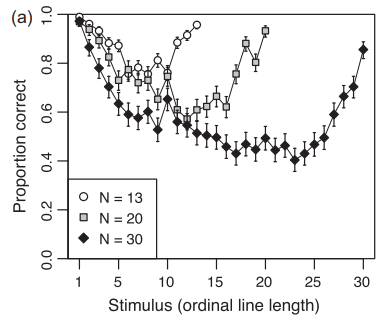
• Bow effect: an absolute identification experiment consists of repeatedly presenting the subject with a randomly chosen stimulus, and asking the subject to respond with his or her best guess regarding the ordinal identity of the stimulus.
• Range effect: as the number of stimuli in the set increases, identification accuracy decreases. Performance remains low even when neighboring stimuli are highly discriminable.

Index of efficiency

\[\epsilon=\frac{D_{\mathrm{emp}}-D_{\max }}{D^{\star}-D_{\max }} \]

where \(D_{emp}\) reflects the empirical distortion according to a given cost function, \(D_{max}\) is the maximum distortion (the point where the rate–distortion curve intercepts the x-axis, or equivalently the optimal ‘guessing’ performance), and \(D^{\star}\) is the minimal distortion for a channel with the same information rate as empirical performance.

Cost function

\[\mathcal{L}_{3}=\left|\alpha_{(y)}-\alpha_{(x)}\right| \]

Implicit cost function

Rate–distortion theory offers a means of recovering (via inverse decision theory) the implicit cost function based on empirical performance.

Perceptual working memory

Introduction

Participants viewed displays containing 1, 2, 4, or 8 line segments of varying length. After a brief memory retention interval, a new ‘probe’ stimulus was displayed at the location formerly occupied by one of the memory items. The participant was asked to report whether the new stimulus was shorter or longer than the remembered item

Cost function

\[\mathcal{L}(x, y)=\frac{|y-x|^{\beta}}{|y-x|^{\beta}+\alpha^{\beta}} \]

The parameters \(\alpha\) and \(\beta\) determine the shape of the cost function. All curves in this family are monotonically increasing and reach an asymptote at 1. The parameter a determines the memory error at which the cost reaches half its maximum, \(L = 0.5\). The parameter \(\beta\) determines the slope or steepness of the cost function.

Result

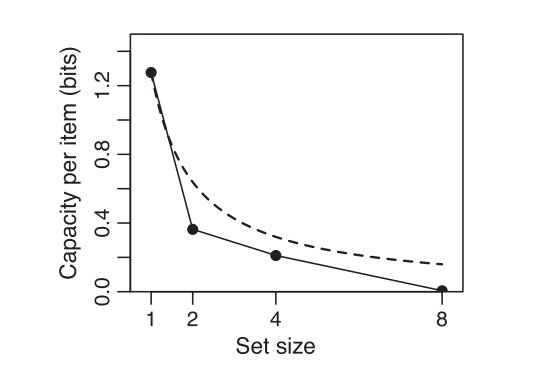
Lastly, different trials of the experiment varied the set size (the number of stimuli that were presented simultaneously). It is to be expected that as more items are held in memory, less capacity will be available to encode or represent each item.

Appendix A

This section briefly describes four approaches to solving rate– distortion problems. A rigorous treatment of the first three approaches can be found in Berger (1971). The final approach described in this section, based on the Blahut algorithm (Blahut, 1972), is also the favored method due to its simplicity, generality, and computational efficiency.

Appendix B

A software package implementing the Blahut algorithm, written in the R programming language, is made available.

标签：function,perception,theory,rate,distortion,Rate,memory
来源： https://www.cnblogs.com/xuzhang/p/15502832.html