首页 > 其他分享> > 高频波动率交易

高频波动率交易

2021-10-20 20:04:09 作者：互联网

https://zhuanlan.zhihu.com/p/408273484

什么是vega?

delta是期权价格对标的敏感度
gamma是期权价格的1%delta的敏感度
vega是期权价格对隐含波动率的敏感度，对spot的二阶统计量

BS公式：

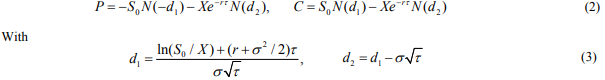
$S_on(d_1)=Xe^{-rt}n(d_2)$ 的证明和推导

Vega求导

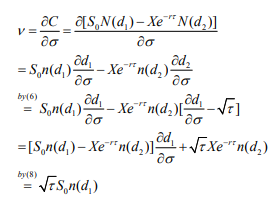
https://core.ac.uk/download/pdf/234629502.pdf

	position	cash position	pnl
delta	delta	delta * spot	delta * spot_change
gamma	gamma * spot^2	gamma * spot^2 / 100	0.5 * gamma * (spot_change)^2
vega	Fe^(-rT) sqrt(T) * pdf(d1)	vega_position * IV%	vega_position * IV_change%

由于 $d1=\frac{ln(S/K)+(r-q+\frac{1}{2}\sigma^2)T}{\sigma\sqrt{T}}$
由于正态分布的 scipy.stats.norm(0,1).pdf(0) = 0.3989
一年期期权的vega约是 $vega \leq 0.4*delta * \sqrt{1}$ ，所以相比delta，vega占的权重还是较小的。
从 $d1$ 的输入，我们可以通过调整拿不同期权 $T$ 和 $\sigma$ 的组合来实现整体想要的 $vega$ 头寸。
通过波动率的预测就可以获取理论期权的价格信号， $\sigma * vega = option\_alpha$

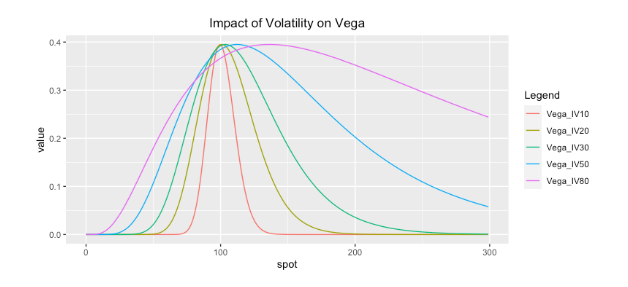
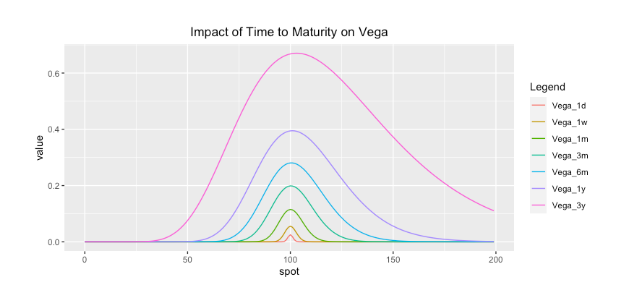
什么是波动率（RV，IV，HV）

在期权交易中，波动率可以当作一个独立的资产来交易
波动率相比资产价格是平稳的，所以提供了时间序列分析的可能性。
波动率短期会聚集，长期会回归，期望值不停漂移，但短期肉眼很难看出哪个会占大头，因此提供了分析不同波动率的估计值提供了做因子预测的可能性
波动率有三种，HV，RV，IV

RV是瞬时或者高频的波动离散率，均值足够低，可用于预测或择时。打破了随机游走的假设。模拟了波动率的高聚集性。根据optiver和kaggle的波动率预测比赛Optiver Realized Volatility Prediction，RV的定义是sqrt(sum(return_list**2)), return_list可以用2个tick算或者4个tick算等等
IV是从期权价格自己推出来的隐含波动率，与期权价格正相关。反映了市场从当下到到期时对期权标的波动率。vega*IV=callprice。对IV有疑问的可以去这里看Charlie：金融衍生品（下）期权模型与策略
HV是波动率的长期回归价值标准，基于股价是随机游走和对数正态分布的假设再做正态收益方差的根号项，在-34%到34%分布区间的概率

二项分布理论上是这样的 $p(k)={n \choose k}p^k(1-p)^{n-k}$ ，p是上涨下跌概率，从k里面选n个trial
然后假设在t时间的股价是根据初始价格和n*t的（50%-50%）coin flip得到的
$S_n(t)=s(0)(1+\frac{\sigma}{\sqrt{n}})^{\frac{1}{2}(nt+M_{nt})}(1-\frac{\sigma}{\sqrt{n}})^{\frac{1}{2}(nt-M_{nt})}$
当n趋近于无穷大的时候， $S(t)=S(0)e^{\sigma W(t)-\frac{1}{2}\sigma^2t}$
这时股价就是以对数正态分布， $log(S_T)\sim N(logS_0+(r-\frac{1}{2}\sigma^2)T,\ \sigma^2T)$ 。另外用对数模拟股价的好处是1.股价不能为负；2.对数收益可以相加；3.对数收益可以低于-100%
因此对数收益为正态， $r = ln(\frac{p_n}{p_{n-1}})-1$ or $r = ln(p_n)-ln(p_{n-1}) -1$
正态分布下的标准差公式， $\sigma = \sqrt{\frac{1}{N-1}\Sigma^N_{i=1}(r_i-\bar{r})^2}$
$\sigma^2=E((r-\bar{r})^2)=E(r^2-2r\bar{r}+\bar{r}^2)=E(r^2)-2E(r)E(\bar{r})+E(\bar{r})^2=E(r^2)-\bar{r}^2$
由于用不同交易日周期计算的短期回归的 $\bar{r}$ 不同，历史波动率也会根据不同计算方法得出的 $\bar{r}$ 波动

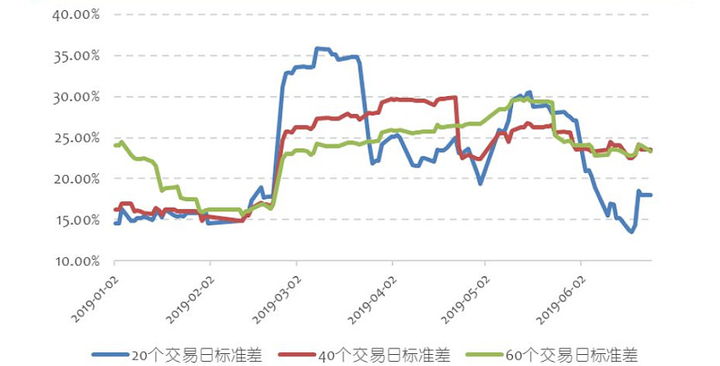
不同瞬时波动率RV的估计值

R是对数正态分布资产价格的正态分布收益

	波动率估计的期望值是Return标准差的多少倍
sqrt(sum(return_list**2))	均值为零的RV定义
\|R\| estimator	0.798*sigma 线性，低估
R^2 estimator	非线性，低估或高估
log(R) estimator	need pro WolframAlpha
First Exit estimator	1.25*sigma 线性，高估，随着样本数变化
Parkinson estimator	0.9*sigma 线性，低估，随着样本数变化 f(n)
GK1980-OHLC estimator	0.9*sigma 线性，低估，随着样本数变化 f(n)
Bollerslev(1998)
Nadaraya-Watson
Tick volume
Yang-Zhang
Rogers-Satchell

由于高频数据中蕴含了比低频数据更多的市场波动信息，因此基于高频数据的波动率测度一定是一种更为真实的市场波动描述。已实现波动率的计算不需要复杂的参数估计方法，无模型、计算简便，在一定条件下是积分波动率(已实现波动率的概率极限)的无偏估计量
当价格分的足够细，高频上波动率本质就是在计算jump/diffusion/noise。低频里当return步长太大波动率会不准，步长太短会被高频的噪音主导。因此普遍的低频RV计算方法是对数价格1天或两天5分钟的差去平方求和
低估说明离散模型无法观测到真实价格的最高和最低值。
n是去实际波动率的样本数
理论上R^2是个很好的短期波动率估计值，因为在高频里回归属性的 $\bar{r}\approx0$ , $\sigma \approx E(r^2)$ 并且是GBM里的quadratic variation
First Exit estimator可以用高频数据来处理jump，通过上下穿barrier来更高估波动率
|R|的期望值计算方法见Sinclair波动率交易书里(公式2.12)绝对收益的期望值是怎么求到的？这个估计值好的原因是它模拟了标的出现大涨或大跌的下一个交易日，波动指数往往会有大的涨幅。其中上涨行情中这一现象会更加明显。

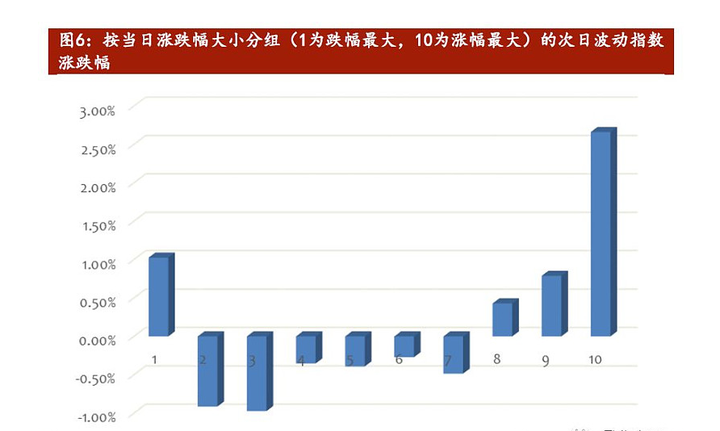
$E(R^2)=\frac{\sqrt{2\pi}}{(\frac{1}{\sigma^2})^\frac{3}{2}}$ 计算方法见WolframAlpha

|R|和|R^2|的波动率估计值在（0.5，0.4相交叉），因此交易员可以根据对实际波动率的解读来改变波动率预测的激进度。0.5倍的真实波动率之下，|R|估计的更高，0.5倍真实波动率之上则R^2的估计更高。

因子预测

（以下结果均出自于超过10w条高频数据样本集）

平值内波动率因子

1. 波动率条件触发型因子

df['sig'] = np.where((df['rolling_vol'] < 10) & (50 < df['rsi']) & (tmp_df['rsi'] < 80), 1, 0)
df['sig'] = np.where((df['rolling_vol'] > 20) & (20 < df['rsi']) & (df['rsi'] < 50), -1, 0)

2. RV，IV，HV，HV_1w，HV_1m等波动率的直接差值预测

假设未来波动率是过去的一定延申
做差值的时候要注意两者的均值是否不同，不然要相应的减去
差值可以用不同的相减，再配上不同的权重
阈值可以用差值的mean
更多的思路可以参考：财通金工的券商研报【财通金工】波动率专题报告之二：随波而动：波动率趋势择时策略投资要点期权世界波动率分为标的波动率与期权隐含波动率期权世界的波动率包括：历史波动率（HV），已实现波动率(RV)，...
下图的具体策略就不详细描述了

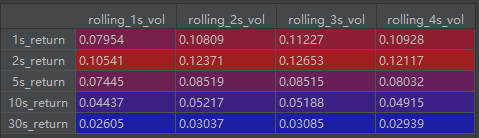
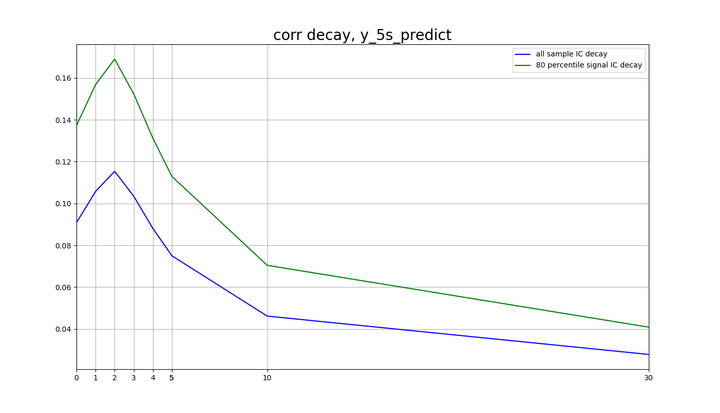
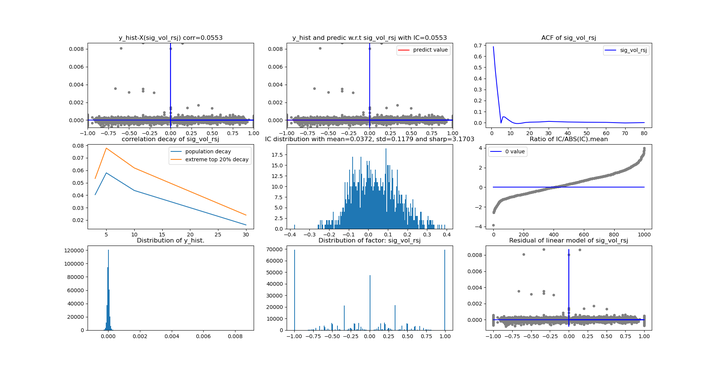
3. 最大似然参数时间序列预测因子

这种因子不用差值，直接用过去的波动率做时间序列预测（>60%相关性），来和未来的回报做IC分析
GARCH：Charlie：复合波动率预测模型
EMEA指数移动平均法，根据历史数据距当前时刻的远近，分别赋予不同的权重，距离现在越近，赋予的权重越大，我们认为越远的历史信息所起的作用越小，因此计算波动率时所赋予的权重越小

4. 离散模型里的LL和RNW波动率估计

stock price vs diffusion return

5. variance swap方差互换波动预期指数

方差互换是远期合约forward的年化方差
Emmanuel Derman P.19-23

平值外波动率因子

5. 根据不同到期日 $T$ 的曲线套利

6. 波动率斜率与行权价套利回归因子（volatility skewness）

根据波动率曲线做整体同个到期日的拟合，从而得到贵的IV和便宜的IV做strike by strike间的套利。这种策略的拟合曲线可以用linear interpolation, cublic spine，wing函数，等画出来，最终回归的时候有几小时到几天不等。

maomao.run：波动率模型（1）Wing Model

一般来说的波动率预测都是平值附近的，乘以vega后也模拟不了波动率微笑。需要用到曲线拟合和插值。但是远期和非平值附近的期权本来交易量和流动性就少，不利于交易与持仓。
用Heston，SABR，stochastic vol inspired，local vol等模型把波动率用行权价log moneyness作为输入计算。
Steven Li：多尺度因子随机波动率模型
local vol模型：Charlie：金融衍生品（下）期权模型与策略
用外汇市场报价方法 $V(K)=V_{atm}+RR(\Delta\sigma_{25})+FLY(\Delta\sigma_{10})$

7. cubicspline回归到taylor expansion

Charlie：隐波会回归到taylor expansion吗？

标签：RV,HV,波动,IV,vega,高频,期权,交易
来源： https://www.cnblogs.com/dhcn/p/15430391.html

高频波动率交易

目录

什么是vega?

什么是波动率（RV，IV，HV）

不同瞬时波动率RV的估计值

因子预测