AGC-002E Candy Piles 画图博弈转化

题意

给定数组\(a\)，每个人轮流操作，每次可以进行两种操作

• 对数组所有非零元素-1
• 将最大元素变为0

直到无法操作游戏结束，最后一次操作的人输

分析

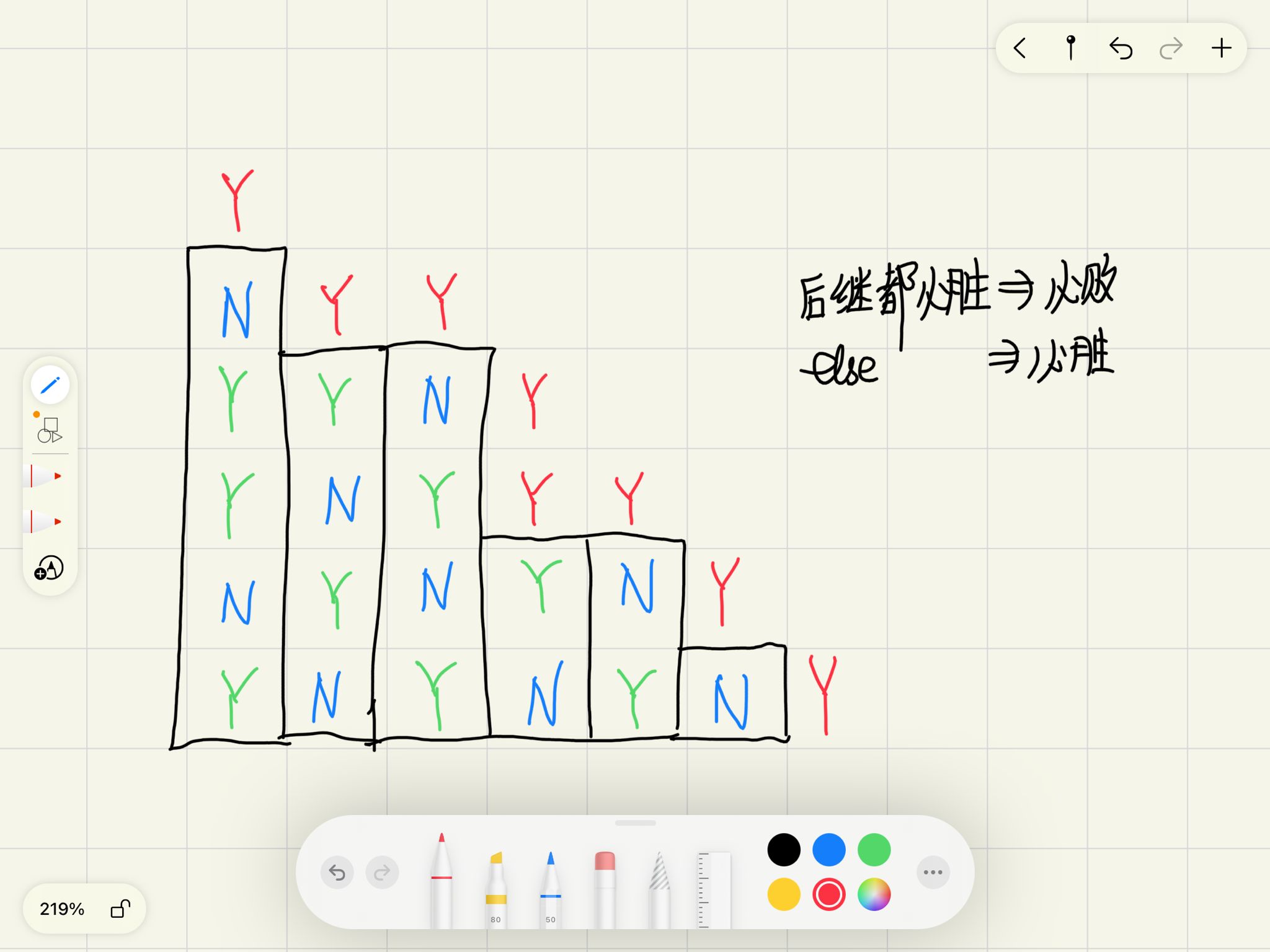
考虑到操作与数的位置无关，考虑把数组排序

每次操作不会改变排序后的大小关系，画成图就是不会改变图的形态

于是操作1可以抽象为从当前点开始，往上走一步 操作2可以抽象为从当前点开始，往右走一步 走完以后的点的右上部分就是当前的形态

显然，最后走到边界外一圈的点是必胜态(因为此题就是无法操作者胜) 那么根据NP引理结合这题最外圈的性质，可以发现每一条主对角线的NP状态相同

实现就可以先找到最大的\((i,i)\)然后根据它往上最多能走的距离和往右最多能走的距离判断这个点的NP状态，这是因为最大的\((i,i)\)往上和往右的NP总是交替的

标签：Piles,AGC,Candy,往右,数组,002E,NP,操作
来源： https://www.cnblogs.com/hznumqf/p/15422360.html