Direct Measure Matching for Crowd Counting

Direct Measure Matching for Crowd Counting

IJCAI 2021

motivation

• 传统高斯处理办法因为高斯核会产生误差，影响精度

Idea

​ 提出了一种新的基于度量的计数方法，将预测的密度图直接回归到散点标注的地面真实值。

• 人群计数是一个度量匹配问题。
• 我们推导了一种半平衡形式的Sinkhorn divergence(发散)，在此基础上设计了一种用于测量匹配的Sinkhorn counting loss.这个新的计算方法放宽了数量约束（两者必须质量相等），完全符合我们的问题假设。
• 我们提出了一个自监督尺度增强机制，using the inter-scale consis- tency in Sinkhorn distance 然后 通过设计一个Sinkhorn尺度一致性损失来抵抗尺度变化。
• 推导了整体损失函数的一阶条件，并引入了缩放迭代进行有效优化，使总损失函数最小

数据集

hanghaiTech、UCF-QNRF、JHU++、NWPU

distance metric 距离度量的选择

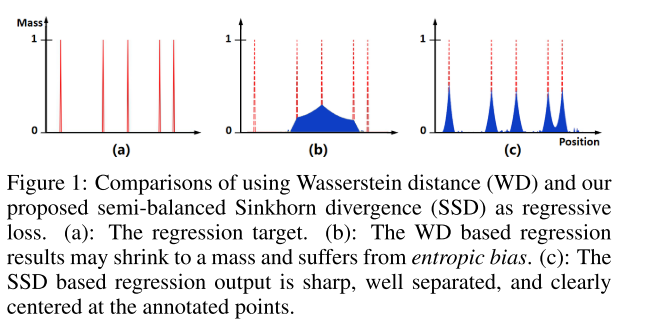
​ 以前都是使用 regularized Wasserstein distance + an entropic function ，熵正则化是为了放松最优运输量分配期间的硬约束，减少计算成本。但是会存在一下两个问题

• 熵项打破了不可分辨的同一性公理，d(x, x) = 0，这是度规空间的基本性质

  the entropic term breaks the the axiom of Identity of indiscernibles

• 优化的质量对熵项的参数设置非常敏感，不适当的熵参数将导致可训练测度收缩到目标重心的质量，种现象通常称为熵偏倚(entropic bias)

  the quality of the optimization is severely sensitive to the parameter set- tings of the entropic term

  

  • Sinkhorn divergence can be an opinion to fix the identity of indiscernibles and the hard constraints issues.

  • Sinkhorn di- vergence is with a self-correcting term.

  Thus it is more stable under different entropic parameters and with a better interpolation meaning, compared to Wasserstein distance

  ​ Sinkhorn divergence 仍然受限制于equivalence of measures’ quantity：这就要求预测密度测量的总量等于地面真实测量的总量，这于人群计数的实际场景不符合。

The Proposed Method

• 结合尺度一致性解释 semi- balanced Sinkhorn divergence
• 解释 传统 Wasserstein and Sinkhorn 评估差异的不足
• 解释 semi-balanced Sinkhorn distance并作为 loss
• 我们采用尺度间一致性机制，将偏差度量为尺度损失。
• 结合这两种损失进行联合回归。

1. Problem Definition

   对于点标注
   
   
   对于密度图
   ​

   因为连续变量和离散变量衡量差异比较有难度，因此 提出新的衡量差异的方法。

2. Wasserstein and Sinkhorn Divergences

   Wasserstein divergence

   ​

   加上熵正则化

   Wasserstein，即在总目标函数中附加一个熵函数作为正则项，以此可以放宽最优传输的严格限制条件，减少计算成本

   ​

   然而，该距离仍存在两个较严重的问题。首先，正则项违反了度量空间中距离自身为零的基本性质，即D(x,x)=0 。其次，最终的优化质量对正则项的参数设置极为敏感，不合适的参数会使度量被训练集中到目标的质心处。这个现象被称为熵偏差。

   Sinkhorn distance

   Sinkhorn 散度可以用来解决距离同一性和相关限制条件问题。与 Wasserstein 距离相比，它有一个自修正项，因此使得 Sinkhorn 散度在不同正则项参数下都保持稳定，具有更好的插值意义。

它仍然受到测度等价性的约束，即预测的密度图总量需要等于标注点，即真实人头总量。

unbalanced assumption的缺点就是认为双方的点都是不确定的，但是点标注的点是确定的。

Semi-balanced Sinkhorn Divergence

这个新散度放宽了对度量等价性的限制，完全符合我们的问题假设

基于上面的分析提出了 Semi-balanced Sinkhorn Divergence

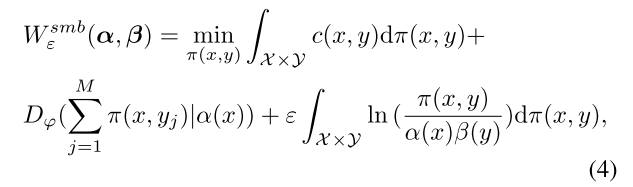
​ D_ϕ是一种传输惩罚，它放松了严格的限制，允许移动质量的量可以不同来测量α。

​

​ semi- balanced Sinkhorn distance

1. Overall loss and Optimization

   

Experimental Results

标签：distance,Direct,正则,balanced,Wasserstein,Counting,Matching,Sinkhorn,度量
来源： https://blog.csdn.net/qq_40889659/article/details/120700272