首页 > 其他分享> > 线性代数——高斯消元

线性代数——高斯消元

2021-09-08 22:01:25 作者：互联网

线性代数——高斯消元

第一板块

首先，我们先来讲解一下线性代数：

什么是线性代数？

函数研究的是，输入一个数，经过函数运算后，产出一个数。而有时候我们研究的问题太复杂，需要输入多个数，经过运算后，就会产出多个数。这时候，线性代数应运而生。

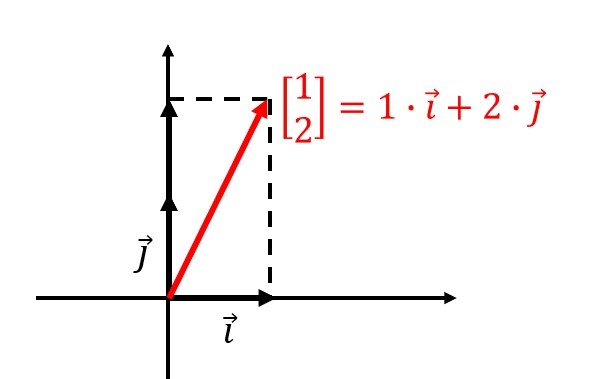
多个数，我们可以用括号括起来，形成一个数组。在几何学上，数组被称作向量，向量就是一个有方向有大小的直线段。

所以，线性代数就是：输入一段直线，经过加工后，产出一段直线

与函数相似，用图来描述就是：
那么矩阵是怎么对直线加工的呢？

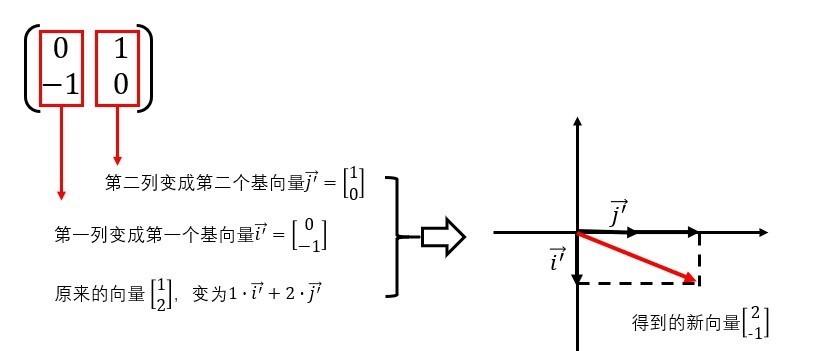
假设输入的直线为【1,2】，用于加工的矩阵为【0, 1，-1, 0】，

那么这个矩阵的加工过程就是把i换成矩阵中的第一列，把j换成第二列，然后再以新的基向量为原料，重新利用【1,2】拼凑一个新的向量。
我们可以用熟悉的口诀“左行乘后列”来检验一下：
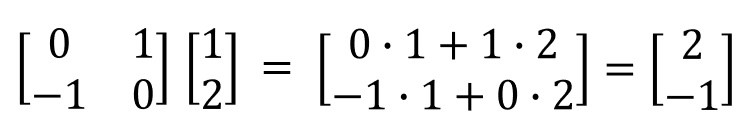
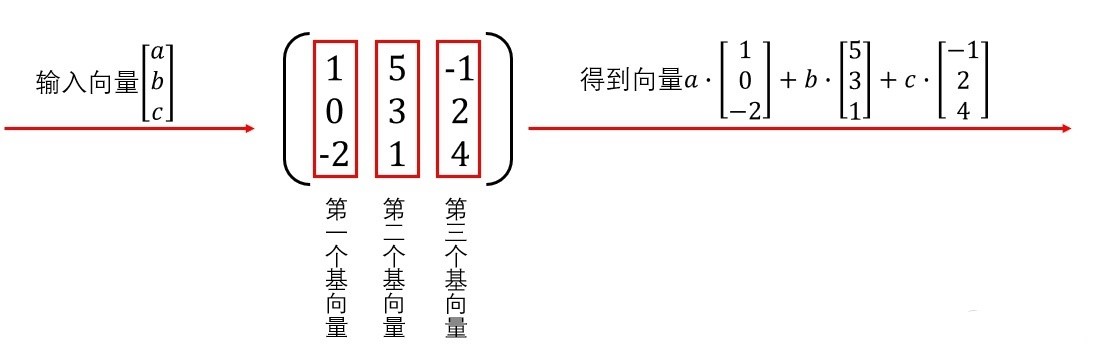
同理，稍微复杂一些的三维向量遇到三维矩阵后的加工过程：
行列式是什么？

矩阵对向量进行加工，行列式能够描述这种加工作用的强弱

上文提到，矩阵对向量加工是通过改变基向量来实现的。以二维为例，默认的基向量张成的面积为1，经过变换后形成的新的基向量张成的面积变为了S，那么这个矩阵的行列式为S
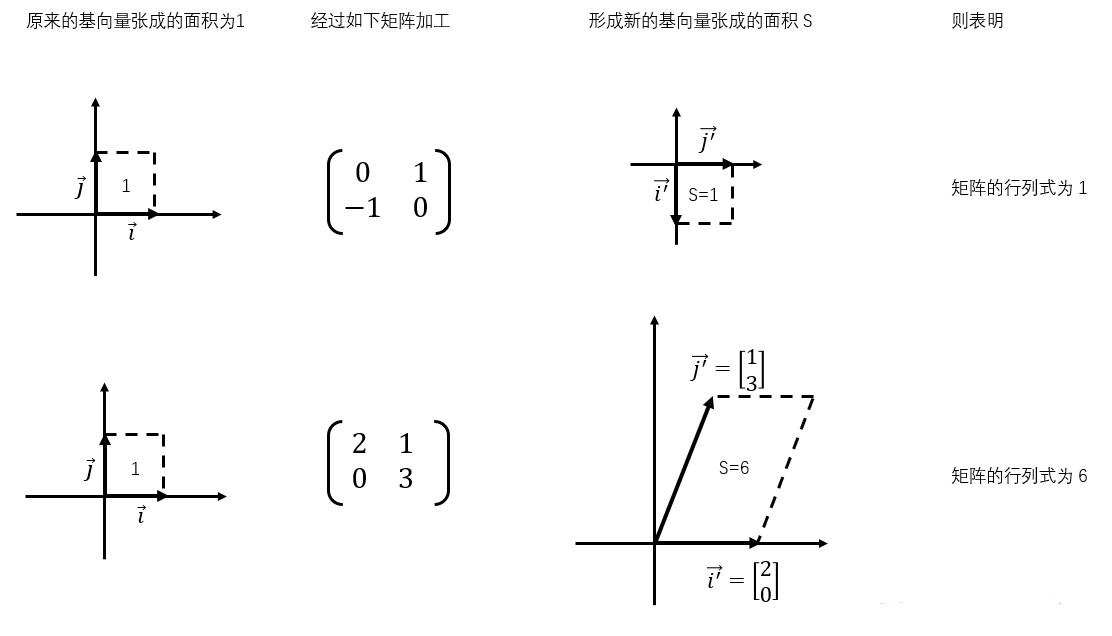
有时候，矩阵的行列式会为0，这就说明新的基向量张成的面积为0，也就说明新的基向量发生了重合。

有时候，矩阵的行列式为负数，说明线性空间发生了翻转。换句话来说，默认的两个基向量，j在i的逆时针方向，经过加工后，线性空间发生了翻转，导致i在j的逆时针方向。
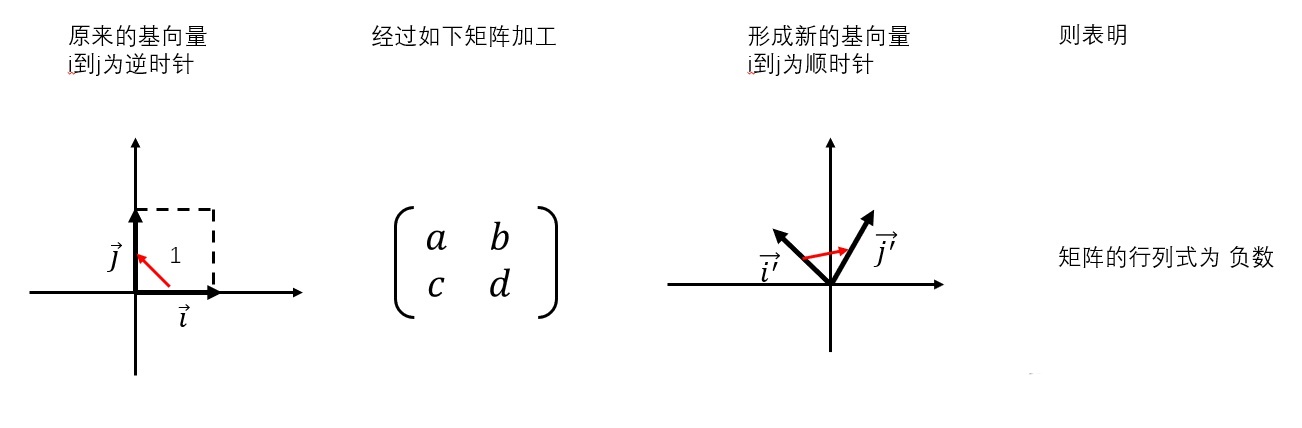
什么是单位矩阵？

就是说无论给它输入什么样的向量，产生的向量都与原来的相同

既然矩阵对向量的加工作用是通过改变基向量来实现的，那么如果想保持你的输入和输出相等，只需要保证矩阵不会改变基向量即可

so，二阶、三阶、以及n阶单位矩阵可写为：
5.什么是逆矩阵？

我们结合图来分析：

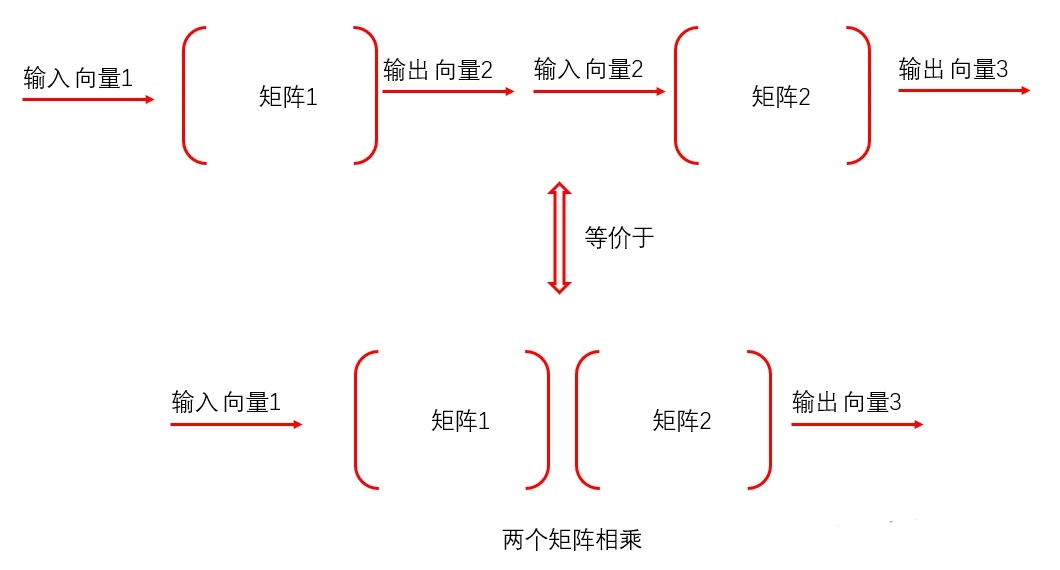
如果说上图向量1等于向量3，那么就说明，向量经过矩阵1和矩阵2后又变成了自己。也就是说，矩阵1和矩阵2的加工作用是相反的（对着干），那么我们就说矩阵1和矩阵2是逆矩阵

明白了原理，那么解逆矩阵就容易了:

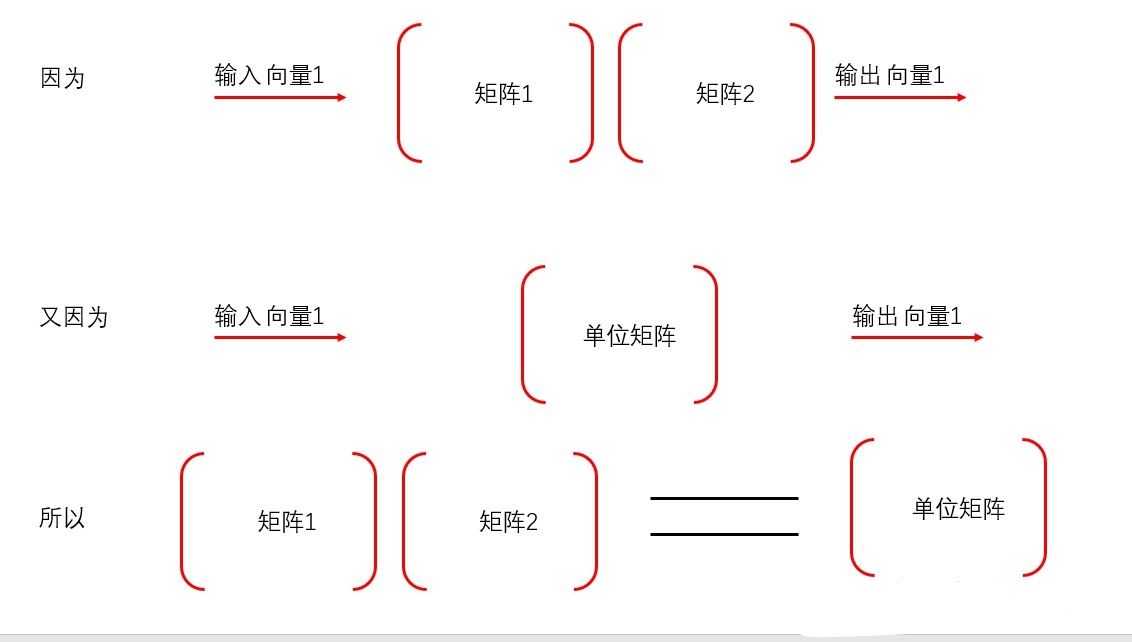
****这里补充一下:行列式为0的矩阵是没有逆矩阵的

因为如果为0，表明矩阵在对向量转换的过程中，将向量空间压缩到了一个更低的维度上。

向量降维后，它就无法还原成原来的样子了。你就好比有一个三维的长方体，从大部分角度来观察，都是一个三维结构，但是，当你正视俯视侧视时，你只能观察到一个二维矩形。我们是无法通过这个二维矩形的样子，来推测出原来的长方体的。

6.什么是秩？

矩阵可以将一个向量进行加工，变成另外一个向量。

就比如说，一个3阶矩阵，可以对多个三维向量进行加工，变成多个新三维向量

有时候，所有的这些新三维向量，最终都落在一条直线上，即1维

有时候，所有的这些新三维向量，最终都落在一个二维平面上，即2维

有时候，所有的这些新三维向量，最终都落三维空间上，即3维

以上三种情况分别对应秩为1,2,3.

总而言之，秩就是描述这个矩阵会不会将输入的向量空间降维。若没有，则称为满秩。

7.什么是特征向量、特征值？

矩阵能够对向量进行加工，变成一个新的向量

但有时候会出现这种情况：

对于某一个矩阵，输入一个向量后，经过加工后，新生成的向量与原来的向量是共线的。那也就是说，这个矩阵在加工的过程中并没有改变其方向

但是虽然不会被改变方向，但是大小改变了，新的向量长度是原来向量长度的λ倍这个λ就是特征向量的特征值

第二板块

明白了什么是线性代数后，我们开始今天的重点——高斯消元（好像前面讲的没有什么用·····，但是打了这么久，就当做给你们普及知识了调皮啦啦啦）

简介

数学上，高斯消元法，是线性代数规划中的一个算法，可用来为线性方程组求解。但其算法十分复杂，不常用于加减消元法，求出矩阵的秩，以及求出可逆方阵的逆矩阵。不过，如果有过百万条等式时，这个算法会十分省时。一些极大的方程组通常会用迭代法以及花式消元来解决。当用于一个矩阵时，高斯消元法会产生出一个“行梯阵式”。高斯消元法可以用在电脑中来解决数千条等式及未知数。亦有一些方法特地用来解决一些有特别排列的系数的方程组。（出自百度。。）

原理

原理其实很简单，就是消元（加减消元&代入消元），所谓消元法，就是将方程组中的一方程的未知数用含有另一未知数的代数式表示，并将其代入到另一方程中，这就消去了一未知数，得到一解；或将方程组中的一方程倍乘某个常数加到另外一方程中去，也可达到消去一未知数的目的。主要用于二元一次方程组的求解。

它的核心呢，就是：

两方程互换，解不变；
一方程乘以非零数k，解不变；
一方程乘以数k加上另一方程，解不变；

分析

obviously，高斯消元是可以用来求n元一次方程组的，它的主要思想就是把一个 n∗(n+1) 的矩阵的对角线消成 1，除了第 n+1 列（用来存放常数项的）的其他全部元素消成 0（方程的系数）

以洛谷的模板题为例（您们可以刷一下）

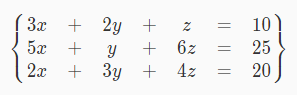
这个三元一次方程组就可以写成如下3 * 4矩阵：

之后运用矩阵的性质（上文提到的核心）来把矩阵消成对角线上的元素为 1，并且除了第 n+1 列其余元素均为 0 的矩阵，

这样我们就很容易的得出每个未知数的值：分别是从上到下第 n+1 列的值（因为这时候每个未知数的系数都为 1，貌似很简单的样子）

那么该如何消呢？（敲黑板！重点来了）

还是以上面的矩阵举例（再放一遍图片）

上面我们提到了要把矩阵消成对角线为 1，除了第 n+1 列其余元素都为 0。那么换句话来说，就是每一列都至少有一个元素不为0，因为若有一列全为0的话，肯定有第i行第i列消不成1，此时是无解的

我们来证明一下：站在方程组的数学角度上来想，我们把每个未知数的系数写成矩阵，所以矩阵的某一列就是某一未知数的全部系数，

如果全为 0，那么不就是没有这个未知数吗？那么这个未知数的值就不能确定了，那不就是无解吗？

ok，明白之后我们就能进行初步判断了：

for(int i=1;i<=n;i++)
    {
        max=i;                      //从第i行开始往下找，一直找到一个第i列不为0的行
        while(a[max][i]==0&&max<=n) 
        max++;                                    
         // 判断第i列元素非0的最上行，因为第i行第i列元素不能为0 
        if(max==n+1) { //一直判到了n+1行，可是一共才只有n行，说明有一列全为0，无解     
		cout<<"No Solution";
		return 0;
	}    
       
        for(int j=1;j<=n+1;j++)            
                //将第i行元素与第max行第i列不为0的那一行与当前行交换 
        swap(a[i][j],a[pl][j]);   //保证第i行第i列不为0
        }

这样之后，我们就保证了第 i 行第 i 列的元素不为 0，可是我们要让第 i 行第 i 列的值整成 1 啊，我们可以用性质 (3)，让第i行的每个元素都除以第 i 行第 i 列的值

注意：这里用到了除法，就有可能出现小数，所以我们要用 double 类型定义二维数组矩阵

	double temp=a[i][i];                         
        for(int j=1;j<=n+1;j++)
        a[i][j]=a[i][j]/temp;

我们就让第 i 行第 i 列的元素搞成 1 列，继续完成接下来的任务：顺便把第 i 列的其他元素搞成 0；

我们已经把第 i 行的搞成了1，所以我们只需要把其余行的每个元素都减去本行的首元素即可（即第 i 行的对应元素）（为什么是第 i 行呢？因为第 i 行第 i 列的元素是 1 啊，比较好消）

代码如下：

#include<bits/stdc++.h>
using namespace std;
int n;
double a[1010][1010];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
       for(int j=1;j<=n+1;j++)
       cin>>a[i][j];
    for(int i=1;i<=n;i++)
    {
        int max=i;
        while(a[max][i]==0&&max<=n) 
        max++;                                    
         // 判断第i列首元素非0的最上行，因为第i行第i列元素不能为0 
        if(max==n+1) {
			cout<<"No Solution";
			return 0;
		}    
        //一直判到了n+1行，可是一共才只有n行，说明有一列全为0，无解 
        for(int j=1;j<=n+1;j++)             //将第i行第i列元素不为0的那一行与当前行交换 
        swap(a[i][j],a[max][j]);
        double temp=a[i][i];                          //让第i行每个元素都除以a[i][i]使得a[i][i]为1 
        for(int j=1;j<=n+1;j++)
        a[i][j]=a[i][j]/temp;   
        for(int j=1;j<=n;j++)
        {
            if(i!=j)                        //将第i列除了第i行的元素全消成0 
            {                               //方法是第j行每个元素a[j][k]都减去a[j][1]*a[i][k] 
                double t=a[j][i];
                for(int k=1;k<=n+1;k++)
                a[j][k]=a[j][k]-t*a[i][k];
            }
        }
    }
    for(int i=1;i<=n;i++)
    printf("%.2lf\n",a[i][n+1]);
    return 0;
}

~~完结撒花~~

好吧，并没有。。。

突然发现这题用高斯约旦消元更简单

高斯约旦消元同高斯消元大体差不多，但消元时上面计算过的行也要消去当前列，最后得到的是对角矩阵而不是上三角矩阵。

相对于传统的高斯消元，约旦消元法的精度更好、代码更简单，没有回带的过程。

约旦消元法大致思路如下：

1.选择一个尚未被选过的未知数作为主元，选择一个包含这个主元的方程。

2.将这个方程主元的系数化为1。

3.通过加减消元，消掉其它方程中的这个未知数。

4.重复以上步骤，直到把每一行都变成只有一项有系数。

我们用矩阵表示每一项系数以及结果

代码如下：

#include<bits/stdc++.h>
using namespace std;
double a[300][300];
int n;
int main()
{
	cin>>n;
	for( int i=1;i<=n;i++)
	{
		for( int j=1;j<=n+1;j++)
		{
			cin>>a[i][j];
		}
	}
	for( int i=1;i<=n;i++)//枚举列（项） 
	{
		 int max=i;
		for( int j=i+1;j<=n;j++)//找出每一列的最大主元 (最大项)
		{
			if(fabs(a[j][i])>fabs(a[max][i]))//找寻最大主元 (最大项） 
            //fabs是取浮点数的绝对值的函数
			{
				max=j;
			}
		}
		if(i^max)//相当于i!=max，保证不在当前行 
		{
			swap(a[i],a[max]);//交换行 
		}
		if(!a[i][i])//主元等于0则说明该列都为0，肯定无解 
		{
			cout<<"No Solution"<<endl;
			return 0;
		}
		for( int j=1;j<=n;j++)//每一项都减去一个数（即加减消元）
		{
			if(j!=i)//对角主元不变 
			{
				 double temp=a[j][i]/a[i][i];
				for( int k=i;k<=n+1;k++)
				{
					a[j][k]-=a[i][k]*temp;
				}
			}
		}
	}

	for( int i=1;i<=n;i++)
	{
		printf("%.2lf\n",a[i][n+1]/a[i][i]);
	}
	return 0;
}

完结撒花~~~~（这次是真完结了）

写的不好，如有错误，请dalao指出······

标签：未知数,int,矩阵,方程,线性代数,高斯消,向量
来源： https://www.cnblogs.com/fzh050919/p/15244731.html