首页 > 其他分享> > LYOI2021 欢乐模拟赛解题报告

LYOI2021 欢乐模拟赛解题报告

2021-09-03 20:04:04 作者：互联网

LYOI2021 欢乐模拟赛解题报告。

A(Alive)

得分情况

全场共 \(21\) 个 \(AC\)，得分率最高。

题解

读入 \(8\) 门科目的分数并累加，与 \(m\) 作比较即可。

#include <bits/stdc++.h>
using namespace std;
int m, x, ans;
int main() {
    cin >> m;
    for (int i = 1; i <= 8; i++) {
        cin >> x;
        ans += x;
    }
    if (ans < m)
        cout << "Die";
    else
        cout << "Live";
    return 0;
}

注意：

\(ans\) 一定要设置初值或者放到全局变量。
不要少读入数啊，考场上有好几位老哥读入都没全。
开数组尽量开大，有一位老哥开 \(8\) 位数组越界了，全 \(TLE\) 了。

B(Base)

得分情况

应该是全场第二简单的题了啊，怎么 \(AC\) 的人这么少啊。

题解

考虑开一个 bool 数组存出现的题目，每读入一个数都把对应的元素设为 true，最后扫一遍数组，统计 true 的个数。

#include <bits/stdc++.h>
using namespace std;
int q, n, m, ans, x;
bool b[10000005];
int main() {
    cin >> q >> n >> m;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &x);
        b[x] = true;
    }
    for (int i = 1; i <= m; i++) {
        scanf("%d", &x);
        b[x] = true;
    }
    for (int i = 1; i <= q; i++) {
        if (b[i] == true)
            ans++;
    }
    cout << ans;
    return 0;
}

C(Calculation)

得分情况

惨不忍睹。

题解

高精度板子。学过没写出来的自己反思一下。。

class High_Accuracy_Algorithm {
private:
    bool cmp(string a, string b) {
        if (a.size() < b.size())
            return true;
        if (a.size() > b.size())
            return false;
        return a < b;
    }

public:
    void Carry(string &c, int t) {
        for (; t < c.size(); t++) {
            if (c[t] - '0' >= 10) {
                int size_s = 0;
                int sum_s = c[t + size_s] - '0';
                while (sum_s) {
                    if (size_s == 0)
                        c[t] = sum_s % 10 + '0';
                    else
                        c[t + size_s] += sum_s % 10;
                    sum_s /= 10;
                    size_s++;
                }
            } else
                break;
        }
    }

    string Add(string a, string b) {
        string c(max(a.size(), b.size()) + 1, '0');
        reverse(a.begin(), a.end());
        reverse(b.begin(), b.end());
        if (a.size() < b.size())
            a.insert(a.end(), b.size() - a.size(), '0');
        else if (b.size() < a.size())
            b.insert(b.end(), a.size() - b.size(), '0');
        for (int i = 0; i < a.size(); i++) {
            int size = 0;
            int sum = a[i] - '0' + b[i] - '0';
            while (sum) {
                c[i + size] += sum % 10;
                if (c[i + size] - '0' >= 10)
                    Carry(c, i + size);
                size++;
                sum /= 10;
            }
        }
        reverse(c.begin(), c.end());
        c = c.substr(c.find_first_not_of('0'));
        return c;
    }

    string Less(string a, string b) {
        if (a == b)
            return "0";
        bool flag = false;
        string c(max(a.size(), b.size()) + 1, '0');
        if (cmp(a, b)) {
            swap(a, b);
            flag = true;
        }
        reverse(a.begin(), a.end());
        reverse(b.begin(), b.end());
        b.insert(b.end(), a.size() - b.size(), '0');
        for (int i = 0; i < a.size(); i++) {
            if (a[i] < b[i]) {
                for (int j = i + 1; j < a.size(); j++) {
                    if (a[j] >= '1') {
                        a[j] -= 1;
                        for (int t = j - 1; t > i; t--) a[t] = '9';
                        a[i] += 10;
                        break;
                    }
                }
            }
            c[i] += a[i] - b[i];
        }
        reverse(c.begin(), c.end());
        c = c.substr(c.find_first_not_of('0'));
        if (flag)
            c.insert(c.begin(), '-');
        return c;
    }

    string Multiply(string a, string b) {
        if (cmp(a, b))
            swap(a, b);
        string c(a.size() + b.size() + 1, '0');
        reverse(a.begin(), a.end());
        reverse(b.begin(), b.end());
        for (int i = 0; i < b.size(); i++) {
            for (int j = 0; j < a.size(); j++) {
                int size = 0;
                int sum = (b[i] - '0') * (a[j] - '0');
                while (sum) {
                    c[i + j + size] += sum % 10;
                    if (c[i + j + size] - '0' >= 10)
                        Carry(c, i + j + size);
                    size++;
                    sum /= 10;
                }
            }
        }
        reverse(c.begin(), c.end());
        c = c.substr(c.find_first_not_of('0'));
        return c;
    }
};

string str1, str2;
High_Accuracy_Algorithm demo;

int main() {
    cin >> str1 >> str2;
    cout << demo.Add(str1, str2) << endl;
    cout << demo.Less(str1, str2) << endl;
    cout << demo.Multiply(str1, str2) << endl;
    return 0;
}

D(Difficulty)

\(70pts\)

对于每一次询问暴力跳父亲节点看结果即可，期望得分\(70\)

\(100pts\)

考虑预处理，定义一个标记数组，初始全部为 \(1\)

先对树做一次先序遍历，如果遇到一个点是特殊节点，那么他子树内所有节点一定要经过特殊节点才能到达根节点，故将其本身与其子树内所有节点标记为 \(0\)

最后对每次询问输出其标记

\(P.S.\)

设\(T\)是有根树，\(a\)是\(T\)中的一个顶点，由\(a\)以及\(a\)的所有后裔（后代）导出的子图称为有向树T的子树。

例如下图

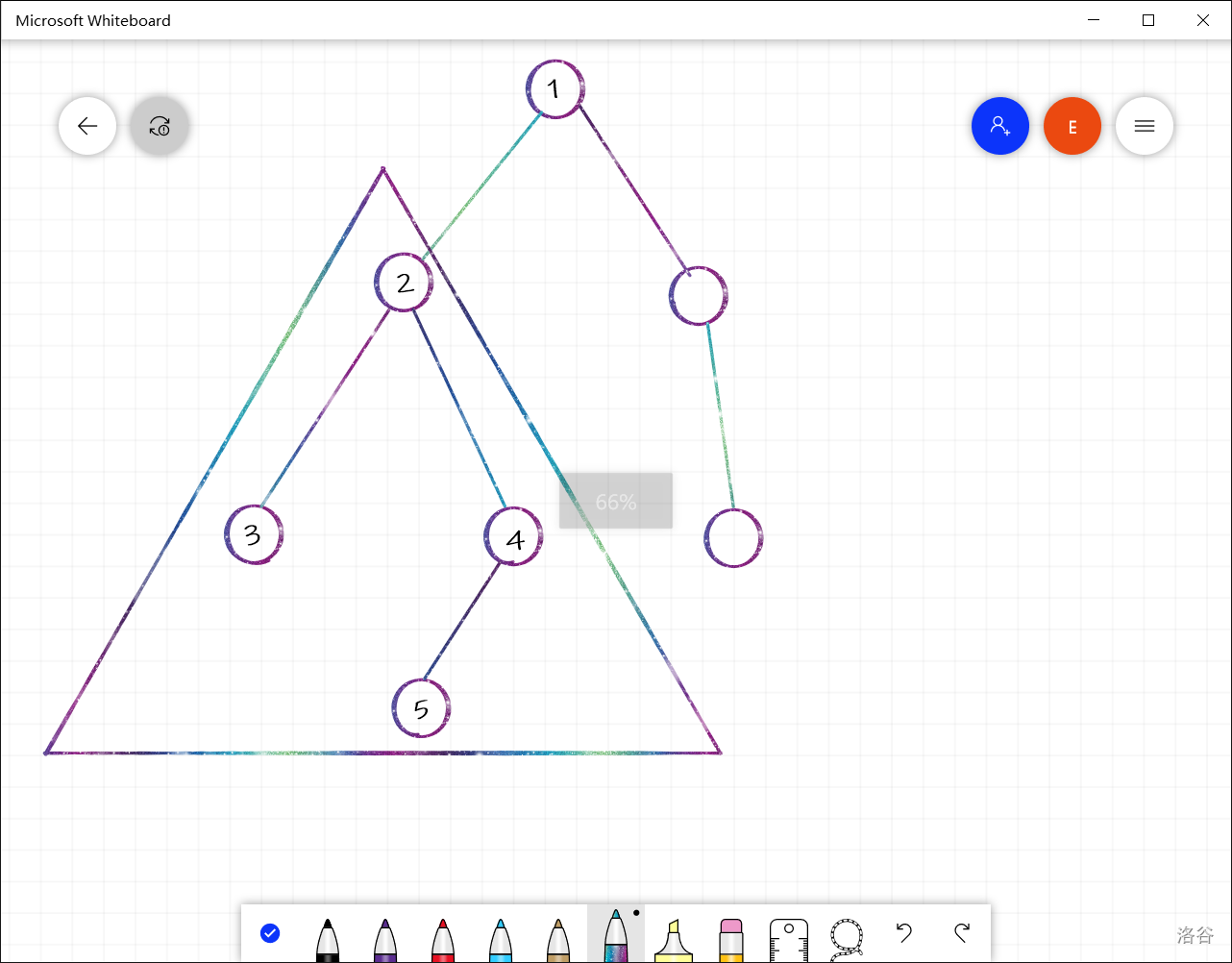
我们称三角形区域为二号节点的子树

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 7;
int fa[MAXN], ls[MAXN], rs[MAXN];
bool spe[MAXN];
bool could[MAXN];
int n, m, q;
bool flag;
void dfs(int u) {
    // cout<<u<<endl;
    if (!u)
        return;
    bool k = flag;
    if (spe[u] == 1)
        flag = 0;
    could[u] = flag;
    if (ls[u])
        dfs(ls[u]);
    if (rs[u])
        dfs(rs[u]);
    flag = k;
}
int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i < n; i++) {
        int u, v;
        scanf("%d%d", &u, &v);
        fa[v] = u;
        if (!ls[u]) {
            ls[u] = v;
        } else {
            rs[u] = v;
        }
    }
    for (int i = 1; i <= m; i++) {
        int y;
        scanf("%d", &y);
        spe[y] = 1;
    }

    if (spe[1] == 0)
        flag = 1;
    else
        flag = 0;
    dfs(1);

    while (q--) {
        int x = 0;
        scanf("%d", &x);
        printf("%d\n", could[x]);
    }
    return 0;
}

E(Explore)

题解

此题为 \(BFS(广度优先搜索)\) 模板题。

核心代码：

void bfs() {
    q[tail][1] = sx;
    q[tail][2] = sy;
    q[tail][3] = 0;
    while (head <= tail) {
        int x = q[head][1], y = q[head][2], cnt = q[head][3];
        if (x == tx && y == ty) {
            printf("%d", cnt);
            exit(0);
        }
        head++;
        for (int i = 0; i < 4; i++) {
            if (a[x + dx[i]][y + dy[i]] == true) {
                tail++;
                q[tail][1] = x + dx[i];
                q[tail][2] = y + dy[i];
                q[tail][3] = cnt + 1;
                a[x + dx[i]][y + dy[i]] = false;
            }
        }
    }
}

F(Formula)

题解

本题考查对数据结构·栈的认识。利用栈保存数字，在遇到运算符时取栈顶的两个元素进行运算后再放回栈顶即可。

读入方面，不做处理，而是放到后面，在运算的同时进行处理。

数据处理。乘10的幂，将字符转换为十进制数，放入栈内。

运算——遇到运算符时，取出栈顶元素进行运算。注意：由于栈先进后出的特点，做除法要用第二次取出的元素去除以第一次取出的元素。

最后输出即可。

#include<iostream>
#include<cstdio>
using namespace std;
long long stk[1000];
int main(){
	long long i=0,now=0;
	char op;
    while((op=getchar())!='@'){
        if(op>='0'&&op<='9') now*=10,now+=op-'0';
        else if(op=='.'){
            stk[++i]=now;
            now=0;
        }
        else if(op=='+'){
            stk[i-1]=stk[i-1]+stk[i];
            stk[i]=0;
            i--;
        }
        else if(op=='-'){
            stk[i-1]=stk[i-1]-stk[i];
            stk[i]=0;
            i--;
        }
        else if(op=='*'){
            stk[i-1]=stk[i-1]*stk[i];
            stk[i]=0;
            i--;
        }
        else if(op=='/'){
            stk[i-1]=stk[i-1]/stk[i];
            stk[i]=0;
            i--;
        }
    }
    cout<<stk[1];
    return 0;
}

补充知识：C++ 自带模板库 STL 中有封装好的栈。我们可以用 STL 快速的通过这道题。

#include <bits/stdc++.h>
using namespace std;
stack<int> n;//STL里的栈，声明格式:stack<数据类型> 栈名称;
char ch;
int s,x,y;
int main()
{
    while(ch!='@')
    {
        ch=getchar();
        switch(ch)
        {
            case '+':x=n.top();n.pop();y=n.top();n.pop();n.push(x+y);break;
            case '-':x=n.top();n.pop();y=n.top();n.pop();n.push(y-x);break;
            case '*':x=n.top();n.pop();y=n.top();n.pop();n.push(x*y);break;
            case '/':x=n.top();n.pop();y=n.top();n.pop();n.push(y/x);break;
            case '.':n.push(s);s=0;break;
            default :s=s*10+ch-'0';break;
        }
        //n.top():返回栈顶元素
        //n.pop():弹出栈顶元素
        //n.push(x):把x压入栈
    }
    printf("%d\n",n.top());
    return 0;
}

G(Generating function)

题解

不难发现如果 \(l\leq \lfloor \frac{r}{2}\rfloor+1\)，那么 \(r \% \left(\lfloor\frac{r}{2}\rfloor+1\right)=\lfloor\frac{r-1}{2}\rfloor\)。可以证明，这是最大的可能答案。

同时，让区间不包含数字 \(\lfloor\frac{r}{2}\rfloor+1\)，即 \(l>\lfloor\frac{r}{2}\rfloor+1\)。可以成名最大答案是 \(r \% l = r - l\)。

时间复杂度为 \(O(1)\)。

#include <bits/stdc++.h>

using namespace std;
#define ll long long

int main() {
    int t;
    std::cin >> t;
    while (t--) {
        ll l, r;
        cin >> l >> r;
        if (r < 2 * l)
            std::cout << r % l << "\n";
        else {
            ll x = (r + 1) / 2;
            std::cout << x - 1 << "\n";
        }
    }
    return 0;
}

标签：10,end,string,LYOI2021,sum,int,解题,欢乐,size
来源： https://www.cnblogs.com/w-rb/p/15224706.html

LYOI2021 欢乐模拟赛 解题报告

A(Alive)

得分情况

题解

B(Base)

得分情况

题解

C(Calculation)

得分情况

题解

D(Difficulty)

\(70pts\)

\(100pts\)

\(P.S.\)

E(Explore)

题解

F(Formula)

题解

G(Generating function)

题解

LYOI2021 欢乐模拟赛解题报告