「CEOI2020」象棋世界 题解
作者:互联网
「CEOI2020」象棋世界 题解
\(~~~~\) 自由复习肯定是做多合一效率最高(雾
题意
\(~~~~\) 给出一个 \(n\) 行 \(m\) 列的棋盘,并给出五种棋子(兵、车、象、后、王
注意到它没有马),\(q\) 次询问求将某种棋子从 \((1,x)\) 移动至 \((n,y)\) 的可达性及在可达时的最少步数和在最少步数下的方案数。(步数是指移动次数)\(~~~~\) \(2\leq m\leq 1000\) ,\(m\leq n\leq 10^9\) ,\(1\leq q\leq 1000\) 。
本文版权归Azazel与博客园共有,欢迎转载,但需保留此声明,并给出原文地址,谢谢合作。
原文地址:https://www.cnblogs.com/Azazel/p/15064692.html
题解
\(~~~~\) 不难看出肯定五种棋子是要分开做的,所以下面对五种棋子分开做阐释,其中棋子的行走规则会在每个部分的开头进行说明,节约题意的空间。此外,下文在讨论最少步数与方案时默认可达。
\(~~~~\) 本篇题解含有以下元素:分类讨论、贪心、组合数学·插板法、DP、矩阵快速幂、矩阵乘法优化。
\(\sf{Pawn}\)(兵)
行走规则
\(~~~~\) 每次仅能向行号增大的方向前进一格。
可达性
\(~~~~\) 不难发现其列数在行走时不变,故当 \(x=y\) 时即可达,否则不可达。
最少步数与方案
\(~~~~\) 由于每次只能前进一格,故最少步数应为 \(n-1\)。
\(~~~~\) 路线只可能是一条推到底,故方案数应为 \(1\)。
代码
查看代码
if(op[1]=='P')
{
if(x==y) printf("%d 1\n",n-1);
else puts("0 0");
}
\(\sf{Rook}\)(车)
行走规则
\(~~~~\) 每次只能到达同行或同列的某一格。
可达性
\(~~~~\) 车必定可达,不过多赘述。
最少步数与方案
\(~~~~\) 分为两种情况:
- 若 \(x=y\) ,则最少步数应为 \(1\) ,此时只有一种方案。
- 否则,最少步数应为 \(2\) ,且此时有两种方案(先走到 \(n\) 行再走到 \(y\) 列或先走到 \(y\) 列再走到 \(n\) 行)。
代码
查看代码
if(op[1]=='R')
{
if(x==y) puts("1 1");
else puts("2 2");
}
\(\sf{Queen}\)(后)
行走规则
\(~~~~\) 每次只能移动到同行、同列或同一斜线上的某一个。
可达性
\(~~~~\) 后必定可达,不过多赘述。作为车的升级版怎么可能车可达后还不可达?
最少步数与方案
\(~~~~\) 仍然分为两种情况:
- 若 \(x=y\) 或 \(|x-y|=n-1\) ,即一步可达时,最少步数应为 \(1\) ,此时只有一种方案。
- 否则,最少步数应为 \(2\) ,但考虑怎么计算方案。不妨看做在 \((1,x)\) 和 \((n,y)\) 处都有一个后,此时两个后的移动范围的交点即为第一步该后应走的位置,故数出交点个数即可。继续分类讨论:
- 横竖线的交点共 \(2\) 个,其必定存在。
- 下面点的竖线与上面点的斜线、下面点的斜线与上面点的竖线的交点共 \(2\) 个,其必定存在。
- 上面点的斜线与下面点的横线会产生 \(2\) 个交点,但仅当 \(n=m\) 且上下中有一个棋子在边角时可以取得其中 \(1\) 个交点在棋盘内(\(n=m\) 且两个都在边角是一步可达的情况)。
- 判断两个点的斜线的两个交点分别是否在棋盘内。
代码
查看代码
if(op[1]=='Q')
{
if(x==y||Abs(x-y)==n-1) puts("1 1");
else
{
int ret=4;
if(n==m){if(x==1||x==m||y==1||y==m) ret++;}
if(((x+1)&1)==((y+n)&1))//斜线的交点
{
int dis=(n-1-Abs(x-y))>>1;
if(min(x,y)-dis>=1) ret++;
if(max(x,y)+dis<=m) ret++;
}
printf("2 %d\n",ret);
}
}
\(\sf{Bishop}\) (象)
行走规则
\(~~~~\) 每次移动到达同一斜线上的某个点。
可达性
\(~~~~\) 不难发现象只能到达棋盘上同色的格子,两个格子同色的条件翻译过来即为两个格子横纵坐标之和的奇偶性相同。
最少步数与方案
\(~~~~\) 先考虑怎么求最少步数,不难想到一个伪贪心的思路:每次向某条斜线走到底,然后换方向继续走到底。
\(~~~~\) 这样虽然步数会达到最少,但很可能在到达第 \(n\) 行时没有到达甚至可能在极端情况下中途还需要换方向使得我们求出的答案偏小。所以我们把贪心改为:直到移动到一个格子 \((a,b)\) 满足:\(a\geq n\) 且 \(b=y\) 。这样修改为什么是正确的下文将会提到。
\(~~~~\) 那么如何把这个最终落点位置修正到 \((x,y)\) 上呢?注意到如果我们在之前某一条斜线的尽头提前一格转方向,则最终的落点就会横坐标不变,纵坐标 \(-2\) 。记 \(d=\frac{(a-n)}{2}\) 表示需要提前转的格数,则我们可以通过提前某(几)条线的换方向的时间来修正到正确的位置上,且提前的总和为 \(d\) 即可 。
\(~~~~\) 但这样的修正有没有可能使某条线的长度缩短到 \(0\) 呢?的确有这种可能,但在最优方案下一定不存在这样的情况。可以考虑使用反证法,即若某最优方案存在某条线长度 \(L\leq d\) ,则直接将该线换方向会使得步数更少,且最终的落点仍然在 \(n\) 行及以上,与最优方案矛盾。
\(~~~~\) 现在我们已经会了怎么求最少步数 \(Ans1\),并且事实上方案数也呼之欲出。令 \(t=Ans1-1\) 表示需要转向的次数,则我们需要做的是将 \(d\) 次提前转向安排到每次转向上,每次转向可安排多个提前转向。转化为经典的插板模型计算即可。
\(~~~~\) 答案为 \(\begin{pmatrix} t+d-1\\d \end{pmatrix}\) 。但注意到 \(t\) 有可能达到 \(n\) 的级别,\(d\) 只能达到 \(m\) 的级别,故这里只能 \(\mathcal{O(d)}\) 算组合数。同时注意左右都要枚举,在 \(Ans1\) 相同时方案数还要加起来,否则取较小者的方案数。
代码
查看代码
if(op[1]=='B')
{
if(((x+1)&1)!=((y+n)&1)) {puts("0 0");continue;}
if(Abs(x-y)==n-1){puts("1 1");continue;}
/*此处略去两次求Ans1,d的过程*/
printf("%d %lld\n",Ans1,(Tmp+C(d,d+Ans1-2))%MOD);
//Tmp为先前一个方向时的方案数,若另一个方向更优则会被置为0
}
King(王)
行走规则
\(~~~~\) 每次向八连通的格子中走一格。
可达性
\(~~~~\) 王必定可达,不过多赘述。
最少步数与方案
\(~~~~\) 考虑切比雪夫距离的一种定义:国际象棋中王从一个格子走到另一个的最小步数即为两个格子之间的切比雪夫距离。同时由于 \(n\geq m\) ,故 \(n-1\) 必定大于 \(|x-y|\) 。求得 \(Ans1\) 为 \(n-1\) 。
\(~~~~\) 考虑如何计算方案:不难定义一个 \(dp_{i,j}\) 表示从 \((1,x)\) 走到 \((i,j)\) 的方案数,且有:
\[\left\{\begin{array}{l} dp_{i,j}=dp_{i-1,j-1}+dp_{i-1,j}+dp_{i-1,j+1}\ \ \ \ (1 < j < m)\\ dp_{i,j}=dp_{i-1,j}+dp_{i-1,j+1}\ \ \ \ (j=1)\\ dp_{i,j}=dp_{i-1,j-1}+dp_{i,j}\ \ \ \ (j=m) \end{array}\right. \]\(~~~~\) 先不讨论细节,该 \(\texttt{DP}\) 是 \(\mathcal{O(nm)}\) 的,而且还要做 \(m\) 次 QAQ
\(~~~~\) 考虑怎么优化这个 \(\texttt{DP}\) ,注意到这是一个简单的递推,所以我们考虑使用矩阵快速幂优化,则其可以优化到总复杂度 \(\mathcal{O(m^3 \log n)}\),但仍然无法通过。
\(~~~~\) 考虑找规律优化矩乘的 \(m^3\) 。设转移矩阵为 \(A\) ,注意到矩阵快速幂中我们本质上只有两种乘法:
\(~~~~\) 所以我们分别来找能否优化这两个乘法:
\(~~~~\) 首先注意到转移矩阵写出来长这样:(\(dp_{i,S,j}\) 表示从 \((1,S)\) 走到 \((i,j)\) 的方案数)
\[A=\begin{bmatrix} 1&1&0&0&\dots&0&0&0\\ 1&1&1&0&\dots&0&0&0\\ 0&1&1&1&\dots&0&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&0&\dots&0&1&1 \end{bmatrix} \]\(~~~~\) 所以对于第一个乘法,我们只用关注 \(A\) 中所有 \(1\) 即可。复杂度为 \(\mathcal{O(m^2)}\) 。
\(~~~~\) 对于第二个乘法,我们不妨来找一下 \(A^n\) 有什么规律(下图为 \(m=10\) 时 \(A^{3}\) 和 \(A^6\) ):
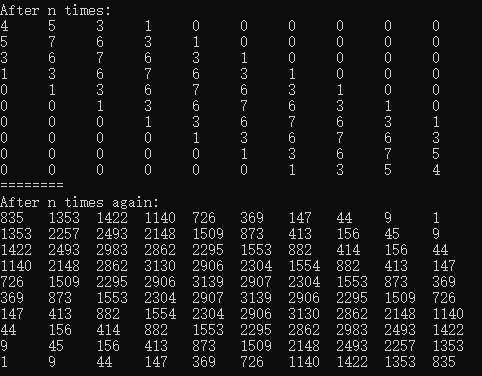
\(~~~~\) 发现以下规律:
- \(A\) 中的元素关于主、副对角线均对称。
- 对于在 \(i\) 行 \(j\) 列的元素,若 \(i+j-1\leq m\) ,则 \(A_{i,j}=A_{i-1,j-1}+{A_{1,i+j-1}}\) 。
\(~~~~\) 若这两个规律成立,则我们可以做到 \(\mathcal{O(m^2)}\) 转移。
\(~~~~\) 第一个规律证明比较简单,在此略过。
\(~~~~\) 第二个规律证明我不会,直接搬别人的:

\(~~~~\) 然后就做完了,复杂度 \(\mathcal{O(m^2\log n)}\)。
\(~~~~\) 当然,上面的递推还有别的利用多项式的做法,但我菜不会。(可以做到 \(\Theta(m \log m \log n+q)\))
代码
查看代码
Matrix Mul1(Matrix A,Matrix B)//A^n->A^{n+1}
{
Matrix ret;
for(int i=1;i<=m;i++)
for(int k=max(i-1,1);k<=min(m,i+1);k++)
for(int j=1;j<=m;j++)
ret.mat[i][j]=(ret.mat[i][j]+A.mat[i][k]*B.mat[k][j]%MOD)%MOD;
return ret;
}
Matrix Mul2(Matrix A,Matrix B)//A^{n}->A^{n+1}
{
Matrix ret;
for(int i=1;i<=1;i++)
for(int k=1;k<=m;k++)
for(int j=1;j<=m;j++) ret.mat[i][j]=(ret.mat[i][j]+A.mat[i][k]*B.mat[k][j]%MOD)%MOD;
for(int i=1;i<=1;i++) for(int j=1;j<=m;j++) ret.mat[j][i]=ret.mat[m-j+1][m-i+1]=ret.mat[m-i+1][m-j+1]=ret.mat[i][j];
for(int i=2;i<=((m+1)/2);i++)
{
for(int j=i;j<=m-i+1;j++)
ret.mat[j][i]=ret.mat[m-j+1][m-i+1]=ret.mat[m-i+1][m-j+1]=ret.mat[i][j]=(ret.mat[i-1][j-1]+ret.mat[1][i+j-1])%MOD;
}
return ret;
}
int P[1000];
Matrix Matrixqpow(Matrix a,ll b)
{
Matrix ret;
for(int i=1;i<=m;i++) ret.mat[i][i]=1;
int cnt;ll tmp=b;
for(cnt=1;tmp;cnt++) P[cnt]=(tmp&1),tmp>>=1;cnt--;
for(int i=cnt;i>=1;i--)
{
ret=Mul2(ret,ret);
if(P[i]) ret=Mul1(a,ret);
}
return ret;
}
if(op[1]=='K')
{
printf("%d ",n-1);
if(AnsK[x][y]) {printf("%lld\n",AnsK[x][y]);continue;}
Matrix zy; zy.Init();
for(int i=1;i<=m;i++)
for(int j=i-1;j<=i+1;j++) if(j>=1&&j<=m) zy.mat[i][j]=1;
zy=Matrixqpow(zy,n-1);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=m;j++) AnsK[i][j]=zy.mat[i][j];
}
printf("%lld\n",AnsK[x][y]);
}
标签:方案,题解,象棋,ret,CEOI2020,leq,最少,步数,dp 来源: https://www.cnblogs.com/Azazel/p/15064692.html