332. 重新安排行程(欧拉回路问题)

题目

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

提示：
如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前
所有的机场都用三个大写字母表示（机场代码）。
假定所有机票至少存在一种合理的行程。
所有的机票必须都用一次 且 只能用一次。

示例 1：
输入：[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
输出：["JFK", "MUC", "LHR", "SFO", "SJC"]

示例 2：
输入：[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出：["JFK","ATL","JFK","SFO","ATL","SFO"]
解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。

深度优先搜索

这道题是要求按字典序的欧拉回路，有以下几个难点：
（1）如何保证得到的欧拉回路按字典序最小？
一种很直接的思路是得到所有欧拉回路然后找到其中字典序最小的那一个。实际上有更简便的方法，可以使得只得到一个欧拉回路，这个欧拉回路就是字典序最小的那一个。

方法是将每个顶点指向的顶点放入最小堆中，我们优先访问字典顺序小的节点ATL即可。因此，我们使用贪心策略，优先访问字典顺序小的顶点。

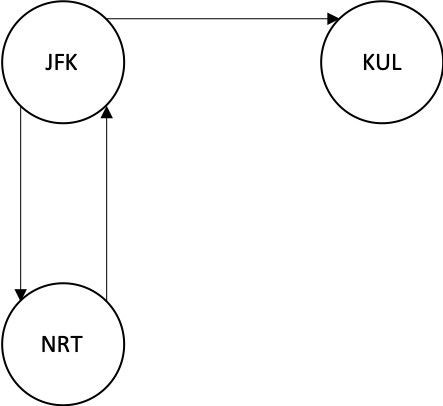
上面例子可以看出，我们别无选择必须先从 JFK 到 NRT 再回 JFK，最后到达 KUL 作为终点。如果我们按照字典顺序先到 KUL，就进入了 “死路”。但是上一个例子我们提到了，优先访问字典顺序小的顶点，那么我们第一次肯定是先到 KUL，这就走不通了，那怎么解决呢？当我们采用 DFS 方式遍历图时，需要将访问到的节点逆序插入到结果集。因此第一个访问到的节点将出现在结果集最后面，而我们是以顺序的方式来查看结果。如果第一个访问的节点是 “孤岛节点”，他会出现在结果集的最后。当我们顺序读取结果集时，这种 “孤岛节点” 是最后遇到的，是图遍历的终点，这样就没有问题了。

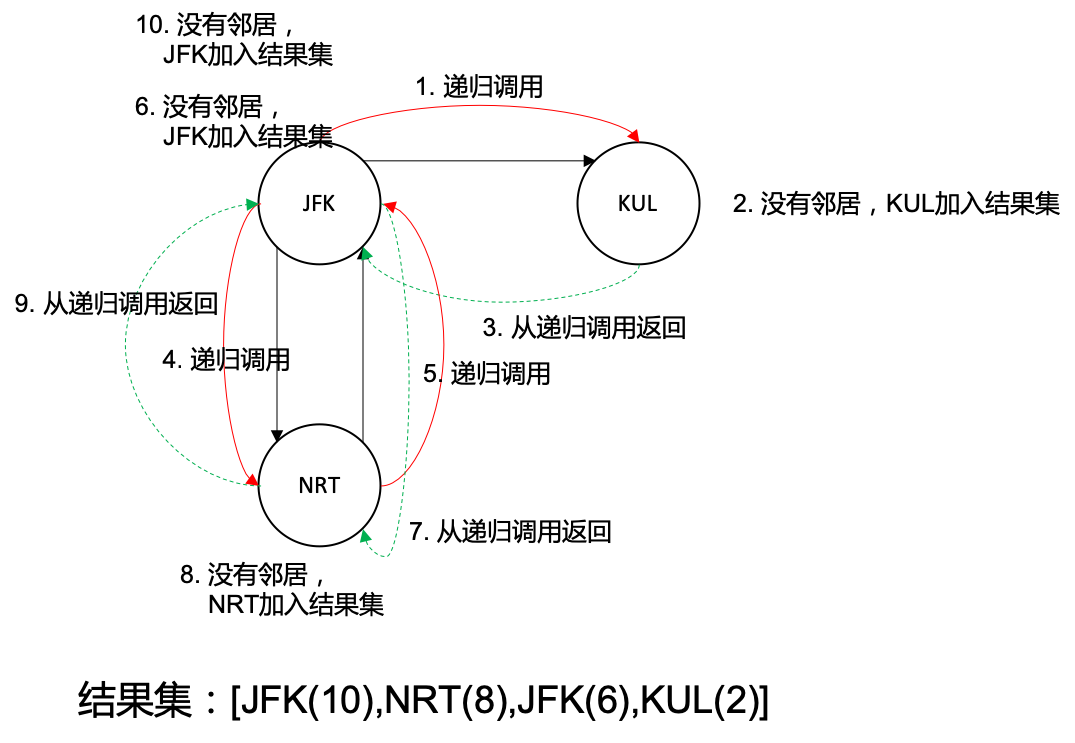
（2）如何标记边为“已访问”？
标记顶点是否已访问容易，但如何标记边已访问呢? 由于整个算法过程只得到一条欧拉回路，也就不需要恢复访问状态的步骤(注意区分DFS和回溯的区别，回溯有恢复状态的步骤)，换句话说，每条边仅经过一次，因此可以用删除边来替代标记。

    private Map<String, PriorityQueue<String>> map = new HashMap<>();

    private List<String> resList = new LinkedList<>();

    public List<String> findItinerary(List<List<String>> tickets) {
        for (List<String> ticket : tickets) {
            String src = ticket.get(0);
            String dst = ticket.get(1);
            if (!map.containsKey(src)) {
                PriorityQueue<String> pq = new PriorityQueue<>();
                map.put(src, pq);
            }
            map.get(src).add(dst);
        }
        dfs("JFK");
        return resList;
    }

    private void dfs(String src) {
        PriorityQueue<String> pq = map.get(src);
        //正常的深度优先搜索步骤
        while(pq != null && !pq.isEmpty()) dfs(pq.poll());
        //当由src发出的边均已访问时，src就成了一个“孤点”，这时把它逆序插入
        resList.add(0,src);
    }

原题：332.重新安排行程
参考：[Java]DFS解法

标签：JFK,src,访问,ATL,332,SFO,重新安排,欧拉,字典
来源： https://www.cnblogs.com/Frank-Hong/p/14886840.html