李宏毅机器学习课程笔记-15.1无监督学习简介
作者：互联网
无监督学习(Unsupervised Learning)可以分为两类：
- 化繁为简
- 聚类(Clustering)
- 降维(Dimension Reduction)
- 无中生有
- 生成(Generation)
在无监督学习(Unsupervised Learning)中，数据集中通常只有\((x,\hat y)\)中的\(x\)或\(\hat y\)，其中：
- 化繁为简就是把复杂的input变成比较简单的output，比如把一堆未标注的“树”图片转变为一棵抽象的“树”，此时数据集只有input \(x\)，而没有output \(\hat y\)。
- 无中生有就是随机给模型一个输入(比如是一个数字)，它就会生成不同图像，此时数据集中没有input \(x\)，而只有output \(\hat y\)
聚类
-
定义
聚类(clustering)就是把"相近"的样本划分为同一类，比如用聚类算法对一些没有标签的图片进行分类，然后人工为这些类别打上cluster 1、cluster 2、cluster 3的标签。
-
一个critical的open question
在聚类算法中要分几个cluster？不能太多也不能太少，需要empirically决定。
-
聚类算法的缺点
它强迫每个样本属于并只属于1个cluster，实际上一个样本可能拥有多个cluster的特征，如果强制把它划分到某个cluster，就会失去很多信息。
如果原先的object是high dimension的，比如image，那现在用它的属性来描述自身，就可以使之从高维空间转变为低维空间，这就是所谓的降维(Dimension Reduction)
K-means
最常用的聚类方法是K-means，其目标为将N个无标签样本\(\{x^1,...,x^n,...,x^N\}\)划分为K个cluster，其算法流程如下：
-
初始化K个cluster的center：\(c^i,i\in \{1,2,...,K\}\)
初始化方法可以是从N个样本中随机选取K个样本作为K个center \(c^i\)的初始值；
如果不从样本中选取center的初始值，最终可能会导致部分cluster中没有样本。
-
遍历所有样本\(x^n\)并判断它属于哪个cluster
如果\(x^n\)与第i个cluster的center \(c^i\)最“接近”，那\(x^n\)就属于该cluster；
我们用\(b_i^n=1\)表示样本\(x^n\)属于第i个cluster，\(b_i^n=0\)表示不属于。
-
更新center：把每个cluster里的所有object取平均值作为新的center值，即\(c^i=\sum\limits_{x^n}b_i^n x^n/\sum\limits_{x^n} b_i^n\)
-
反复第2步和第3步
HAC
HAC的全称是Hierarchical Agglomerative Clustering，它是一种层次聚类算法
假设有5个样本，想要通过HAC进行聚类，其步骤为：
-
build a tree:
过程与哈夫曼树的建树过程类似，只不过哈夫曼树是依据词频建树，而HAC是依据样本相似度建树。
对于所有样本，两两计算相似度并挑出最相似的2个样本，比如样本1和2，将样本点1和2进行merge(比如可以对两个vector取平均)得到代表这2个样本的新“样本”，此时只剩下4个样本，再重复上述步骤合并样本直到只剩下一个样本
-
pick a threshold
选取相似度阈值，形象来讲就是在已构造的tree上横着切一刀，切到的每个“树枝”就是1个cluster，如下图所示。
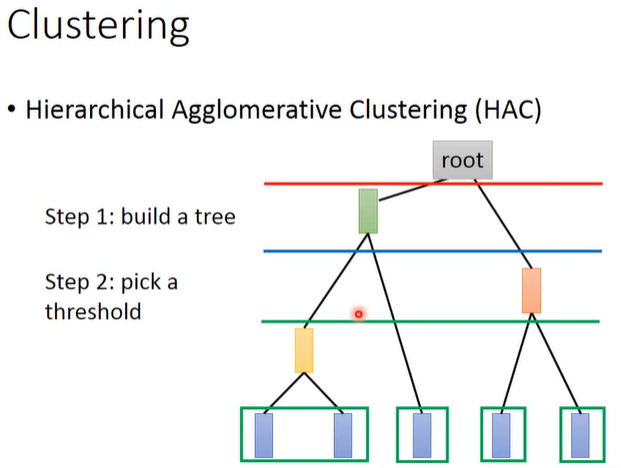
HAC和K-means的最大区别在于如何决定cluster的数量。K-means中需要人工确定cluster数量，而HAC中需要人工确定相似度阈值。
降维
降维即Dimension Reduction。
引入降维
聚类算法的假设是每个样本属于并只属于1个cluster，但实际上一个样本可能拥有多个cluster的特征，如果强制把它划分到某个cluster，就会失去很多信息。所以可以用一个vector来描述1个样本，该vector的每一维表示样本的某一种属性，这种做法就叫Distributed Representation/Dimension Reduction。
降维作用原理
因为数据存在冗余。比如MNIST手写数字图片是28×28的matrix，反过来想，一个任意的28×28的matrix转成图片看起来应该都不会是个数字，或许我们并不需要这么大的数据量来描述数字。
如何实现降维
Dimension Reduction就是要找一个function，其输入是原始的高维特征\(x\)，其输出是降维后的低维特征\(z\)，其中\(z\)的维度数比\(x\)少。
最简单的Dimension Reduction是Feature Selection，即直接将高维数据中一些直观上认为无效的维度删除，这样就做到了降维。但Feature Selection不总是有用，因为很多情况下每个维度其实都不能被直接删除，甚至我们不知道哪些维度可以删除哪些维度不可以删除。
生成
略
Github（github.com）：@chouxianyu
Github Pages（github.io）：@臭咸鱼
知乎（zhihu.com）：@臭咸鱼
博客园（cnblogs.com）：@臭咸鱼
B站（bilibili.com）：@绝版臭咸鱼
微信公众号：@臭咸鱼
转载请注明出处，欢迎讨论和交流!
标签：15.1,HAC,降维,李宏毅,样本,学习,cluster,Reduction,聚类 来源： https://www.cnblogs.com/chouxianyu/p/14879637.html