【匈牙利算法】
作者:互联网
前置
二分图:二分图又称作二部图,是图论中的一种特殊模型。 设\(G=(V,E)\)是一个无向图,如果顶点V可分割为两个互不相交的子集\((A,B)\),并且图中的每条边\((i,j)\)所关联的两个顶点i和j分别属于这两个不同的顶点集\((i\;in A,j\;in B)\),则称图G为一个二分图。
简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
匹配:给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配
极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
求二分图最大匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)
实战
下面好几道(好像总共也没几道题)都是网络流的题 因为数据太水可以用匈牙利水过 emmm大概看一下吧 酒店之王有说明
[hdu2063]过山车
匈牙利算法模板
不断地进行匹配,如果当前匹配不可行,则尝试修改原来的匹配,使得最后的匹配数最大。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=1000+5,M=500+5,inf=0x3f3f3f3f,P=19650827;
int k,n,m,ans,match[N];
double link[N][N],vis[N];
template <class t>void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
bool dfs(int x){
for(int i=1;i<=n;++i){//扫描每个男生
if(link[x][i]&&!vis[i]){//如果能连接 并且i不在当前匈牙利树中
vis[i]=1;
if(!match[i]||dfs(match[i])){match[i]=x;return 1;}
//名花无主或者能腾出空位置来
}
}
return 0;
}
int main(){
while(scanf("%d",&k)!=EOF&&k){
ans=0;
memset(link,0,sizeof(link));
memset(match,0,sizeof(match));
rd(m),rd(n);
for(int i=1,x,y;i<=k;++i) rd(x),rd(y),link[x][y]=1;
for(int i=1;i<=m;++i){
memset(vis,0,sizeof(vis));
if(dfs(i)) ++ans;
}
printf("%d\n",ans);
}
return 0;
}dfs版
>queue Q;
int prev[__maxNodes];
int Hungarian()
{
int ans = 0;
memset(matching, -1, sizeof(matching));
memset(check, -1, sizeof(check));
for (int i=0; i= 0) { // 此点为匹配点
prev[matching[v]] = u;
} else { // 找到未匹配点,即找到增广路
flag = true;
int d=u, e=v;
while (d != -1) {//修改原来的匹配关系
int t = matching[d];
matching[d] = e;
matching[e] = d;
d = prev[d];
e = t;
}
}
}
}
Q.pop();
}
if (matching[i] != -1) ++ans;
}
}
return ans;
}
[SCOI2010]游戏
把各个装备值看作左部点 装备编号看作右部点
(还可以用并查集做 具体看黄学长der
vis太大用memset会超时 从标程上学到 用一个数组gai记录变了的vis 然后初始化时只改变了的
#include<bits/stdc++.h>
using namespace std
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
const int N=1000000+5,M=10000+5,inf=0x3f3f3f3f,P=19650827;
int n,mx,ans,match[N],gai[N];
double vis[N];
template <class t>void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
int head[M],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){
e[++tot]=(edge){v,head[u]},head[u]=tot;
}
bool dfs(int x){
for(int i=head[x],v;i;i=e[i].nxt)
if(!vis[v=e[i].v]){
vis[gai[++gai[0]]=v]=1;
if(!match[v]||dfs(match[v])){match[v]=x;return 1;}
}
return 0;
}
int main(){
freopen("in2.txt","r",stdin);
//freopen("xor.out","w",stdout);
rd(n);mx=ans=0;
for(int i=1,x,y;i<=n;++i) rd(x),rd(y),add(x,i),add(y,i),mx=Max(mx,Max(x,y));
for(int i=1;i<=mx;++i){
for(int i=1;i<=gai[0];++i) vis[gai[i]]=0;gai[0]=0;
if(dfs(i)) ++ans;
else break;
}
printf("%d",ans);
return 0;
}luogu1402酒店之王
一个人有两个要求 若两个要求都满足 则这个人满意
从一个点同时向两边出发 若两个同时满足 则++ans 若不满足 就得把这个点增广出去的边给退回来
但是有bug...主要是这题数据水
(fromluogu讨论区
一组样例:
3 2 2 1 1 1 2 1 1 1 1 1 1 2 1
输出:
2
说明: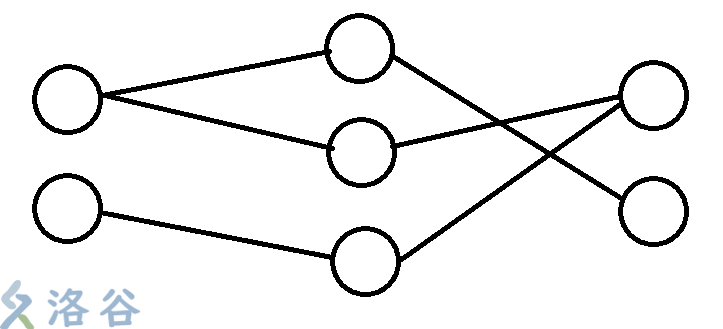 中间的节点表示奶牛,左右表示食物和饮料。
中间的节点表示奶牛,左右表示食物和饮料。
还一组样例:
3 2 2 1 1 1 1 1 1 1 2 1 1 2 1
输出:
2
说明: 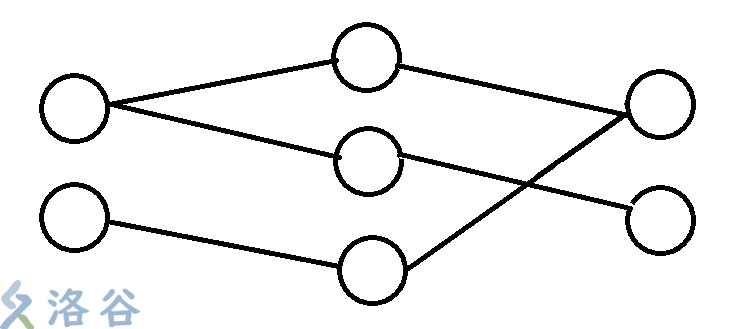
两个样例输出都是2,但匈牙利算法的第二个程序输出结果为1.
结果的差异本质上是代码思路的问题,可以模拟一下程序运行第二组样例的过程
但改一下,可以把luogu2891水过,让连接边最多的牛先去赠广,这样可以避免发生一些不必要的冲突,例如A食物可以同时给牛a和牛b,但是牛a可以匹配更多食物,我们肯定会将食物给牛a,这样再后续的匹配中,答案更优(但还不是最优)
#include<bits/stdc++.h>
using namespace std;
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
const int N=100+5,M=10000+5,inf=0x3f3f3f3f,P=19650827;
int n,p,q,ans,match1[N],match2[N],M1[N],M2[N];
bool vis[N],vis2[N],lka[N][N],lkb[N][N];
template <class t>void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
bool dfs1(int x){
for(int i=1;i<=p;++i)
if(lka[x][i]&&!vis[i]){
vis[i]=1;
if(!match1[i]||dfs1(match1[i])){match1[i]=x;return 1;}
}
return 0;
}
bool dfs2(int x){
for(int i=1;i<=q;++i)
if(lkb[x][i]&&!vis2[i]){
vis2[i]=1;
if(!match2[i]||dfs2(match2[i])){match2[i]=x;return 1;}
}
return 0;
}
int main(){
//freopen("in2.txt","r",stdin);
//freopen("xor.out","w",stdout);
ans=0;
rd(n),rd(p),rd(q);
for(int i=1;i<=n;++i)
for(int j=1;j<=p;++j) rd(lka[i][j]);
for(int i=1;i<=n;++i)
for(int j=1;j<=q;++j) rd(lkb[i][j]);
for(int i=1;i<=n;++i){
memset(vis,0,sizeof(vis));
memset(vis2,0,sizeof(vis2));
for(int i=1;i<=p;++i) M1[i]=match1[i];
for(int i=1;i<=q;++i) M2[i]=match2[i];
if(dfs1(i)&&dfs2(i)) ++ans;
else{
for(int i=1;i<=p;++i) match1[i]=M1[i];
for(int i=1;i<=q;++i) match2[i]=M2[i];
}
}
printf("%d",ans);
return 0;
}[SCOI2001]小狗散步
每两个相遇点之间只能去一个兴趣点而且每个兴趣点只去一次
将每两个相邻的相遇点与其能去的兴趣点连起
然后从相遇点出发做最大二分图匹配 最后输出答案
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
const int N=100+5,M=10000+5,inf=0x3f3f3f3f,P=19650827;
int n,m,ans=0,match[N];
bool vis[N],lnk[N][N];
template <class t>void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
struct node {
int x,y;
}a[N],b[N];
double qdis(node A,node B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}
bool dfs(int x){
for(int i=1;i<=n;++i)
if(lnk[x][i]&&!vis[i]){
vis[i]=1;
if(!match[i]||dfs(match[i])){match[i]=x;return 1;}
}
return 0;
}
int main(){
freopen("in2.txt","r",stdin);
//freopen("xor.out","w",stdout);
rd(n),rd(m);
for(int i=1;i<=n;++i) rd(a[i].x),rd(a[i].y);
for(int i=1;i<=m;++i) rd(b[i].x),rd(b[i].y);
for(int i=1;i<n;++i)
for(int j=1;j<=m;++j)
if(qdis(a[i],a[i+1])*2.0>=qdis(a[i],b[j])+qdis(b[j],a[i+1])) lnk[j][i]=1;
for(int i=1;i<=m;++i){
memset(vis,0,sizeof(vis));
if(dfs(i)) ++ans;
}
printf("%d\n",ans+n);
for(int i=1;i<n;++i){
printf("%d %d ",a[i].x,a[i].y);
if(match[i]) printf("%d %d ",b[match[i]].x,b[match[i]].y);
}
printf("%d %d",a[n].x,a[n].y);
return 0;
}标签:ch,匹配,int,匈牙利,while,算法,include,matching 来源: https://www.cnblogs.com/lxyyyy/p/11393311.html