电影推荐系统---协同过滤算法(SVD,NMF)

SVD

参考 https://www.zybuluo.com/rianusr/note/1195225

1 推荐系统概述

 

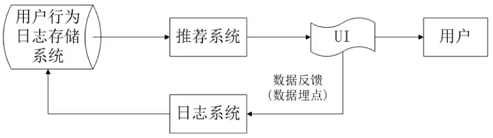
1.1 项目安排

 

 

1.2 三大协同过滤

 

1.3 项目开发工具

 

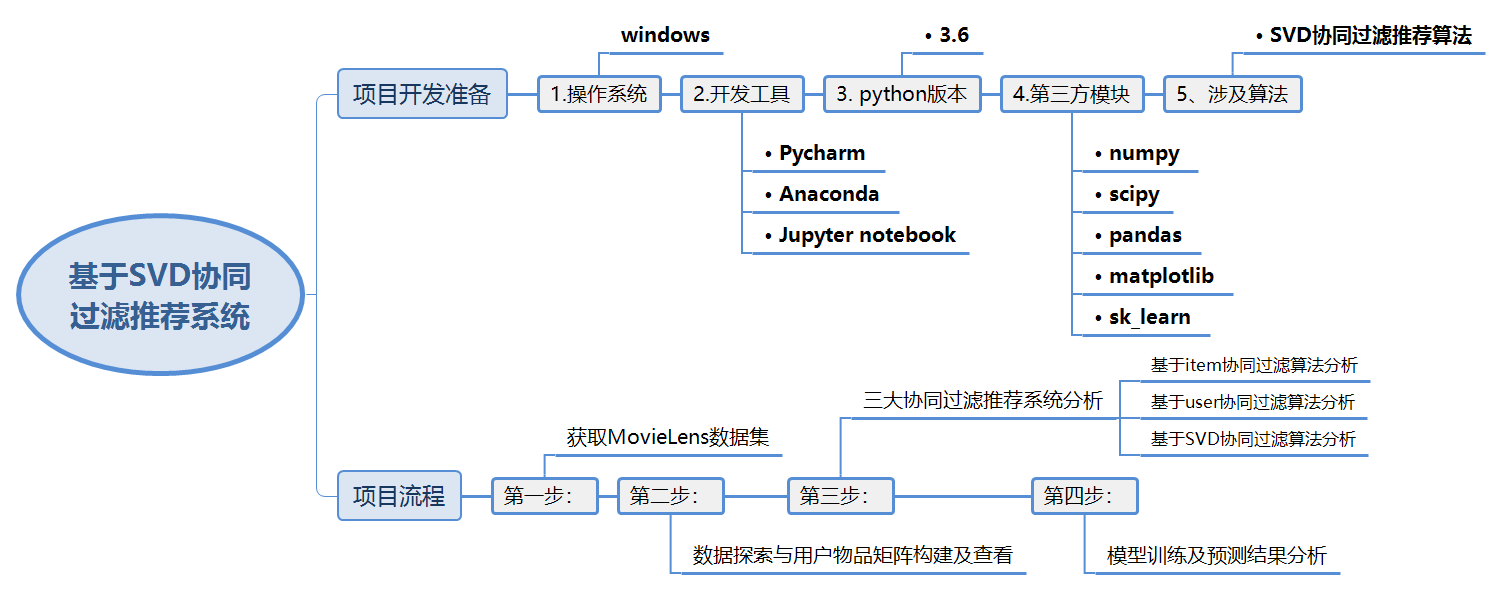
2 Movielens数据集简介

• MovieLens是推荐系统常用的数据集； 
  MovieLens数据集中，用户对自己看过的电影进行评分，分值为1~5； 
  MovieLens包括两个不同大小的库，适用于不同规模的算法； 
  ·小规模的库事943个独立用户对1682部电影做的10000次评分的数据； 
  ·大规模的库事6040个独立用户对3900部电影做的100万次评分的数据；

数据集下载地址：http://files.grouplens.org/datasets/movielens/ml-100k.zip

 

3 数据探索

 

3.1 导入小规模的库数据

 

1. import numpy as np
2. import pandas as pd
3. import matplotlib.pyplot as plt
5. data=pd.read_csv('ml-100k/u.data',sep='\t',names=['user_id','item_id','rating','timestamp'])
6. data.head()

 

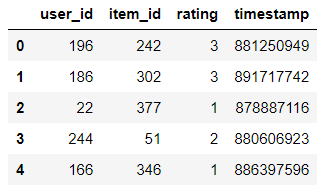
3.2 数据探索及发现

 

1. # 数据信息查看
2. data.info()

 

1. # 数据描述
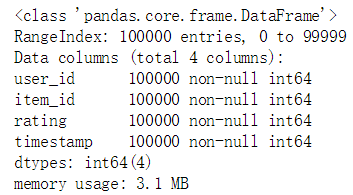
2. data.describe()

 

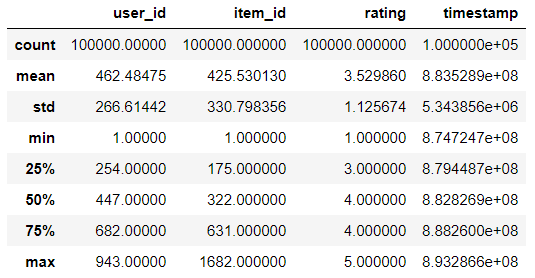
1. data.user_id.nunique() # nunique() --> 返回不重复user_id的个数，统计用户的个数
2. data.item_id.nunique() # 统计被评价电影的个数

>> 943
>> 1682

 

1. data.duplicated(subset=['user_id','item_id']).sum() # 查看user_id与item_id是否有重复的情况

>> 0

从导入的数据可以看出，user_id共有943个，item_id共有1682个，与数据对于的user_id及item_id的编号刚好是1~943和1~1682，可见数据已经清洗好的，不需要重新处理 
然后将数据集拆分为训练集和测试集，分别进行处理 
且user_id与item_id均不存在重复的情况，数据可以直接使用。

 

3.3 数据检查

 

3.3.1 查看每个物品对应用户的数量

 

a. 根据item_id分类聚合

 

1. # 统计每个物品对应的用户数
2. item_id_usercnt = train_data.groupby('item_id').count().user_id
3. item_id_usercnt[:5]

 

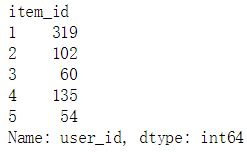
b. 直方图展示

 

1. # 展示分类聚合结果
2. plt.hist(item_id_usercnt.values)
3. plt.show()

 

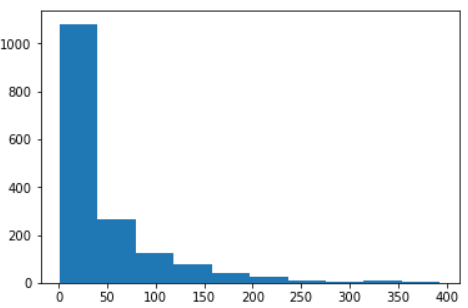
c. 查看十分位数

 

1. # 分别查看每一物品对应的用户的十分位数（十分位数、二十分位数...一百分位数）
2. item_id_usercnt.quantile(q=np.arange(0,1.1,0.1))

 

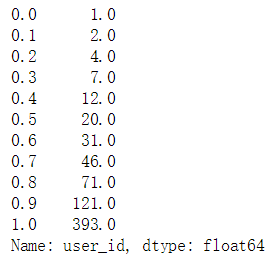
d. 物品对应用户数量数据查看发现

约有30%左右的物品对应的用户数少于10个，对这部分物品计算与其他物品的相似度不会太准确

 

3.3.2 查看每个用户对应物品的数量

 

a. 根据user_id分类聚合

 

1. # 统计每个用户对应的物品数
2. user_id_itemcnt = train_data.groupby('user_id').count().item_id
3. user_id_itemcnt[:5]

 

b. 直方图展示

 

1. # 展示分类聚合结果
2. plt.hist(user_id_itemcnt.values)
3. plt.show()

 

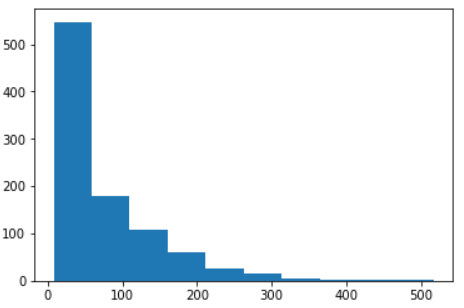
c. 查看十分位数

 

1. # 分别查看每一用户对应的物品的十分位数（十分位数、二十分位数...一百分位数）
2. user_id_itemcnt.quantile(q=np.arange(0,1.1,0.1))

 

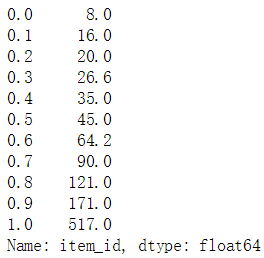
d. 物品对应用户数量数据查看发现

从每个用户对应的物品数量至少为20个的情况来看，基于用户相似度的准确度会比基于物品要好

 

3.4 构建用户-物品矩阵

 

3.4.1 获取矩阵行数m、列数n

 

1. # 通过nunique()方法分别获得user_id、item_id的去重计数
2. m_users = train_data.user_id.nunique() #
3. n_items = train_data.item_id.nunique()

 

3.4.2 创建一个全是0的m*n的矩阵并向矩阵中填充对应数据

 

1. user_item_matrix = np.zeros((m_users,n_items)) # 创建一个全是0的m*n的矩阵
2. '''
3. itertuples() 将每一行转换为对应的元组，且数据一一对应
4. for line in data.head().itertuples():
5. print(line)
6. >> Pandas(Index=0, user_id=196, item_id=242, rating=3, timestamp=881250949)
7. >> Pandas(Index=1, user_id=186, item_id=302, rating=3, timestamp=891717742)
8. >> Pandas(Index=2, user_id=22, item_id=377, rating=1, timestamp=878887116)
9. >> Pandas(Index=3, user_id=244, item_id=51, rating=2, timestamp=880606923)
10. >> Pandas(Index=4, user_id=166, item_id=346, rating=1, timestamp=886397596)
11. '''
12. for line in data.itertuples():
13. user_item_matrix[line[1]-1,line[2]-1]=line[3]
14. '''
15. 因为user_id 和 item_id都是从1开始编号的，而矩阵的索引是从零开始
16. data数据的第二列为user_id，第三列为item_id，第三列则为对应user对item的评分
17. '''
18. user_item_matrix #展示一下用户物品矩阵

 

3.4.3 查看用户-物品矩阵的稀疏性

 

1. # 统计矩阵中非0值的个数与矩阵总元素个数的比值，保留3位小数
2. sparsity = round(len(user_item_matrix.nonzero()[1])/float(m_users*n_items),3)
3. sparsity

>> 0.063

 

发现：用户-物品 矩阵非常稀疏，只有6%的用户物品有互动记录

 

4 基于item的协同过滤推荐系统

 

4.1 物品相似度矩阵

 

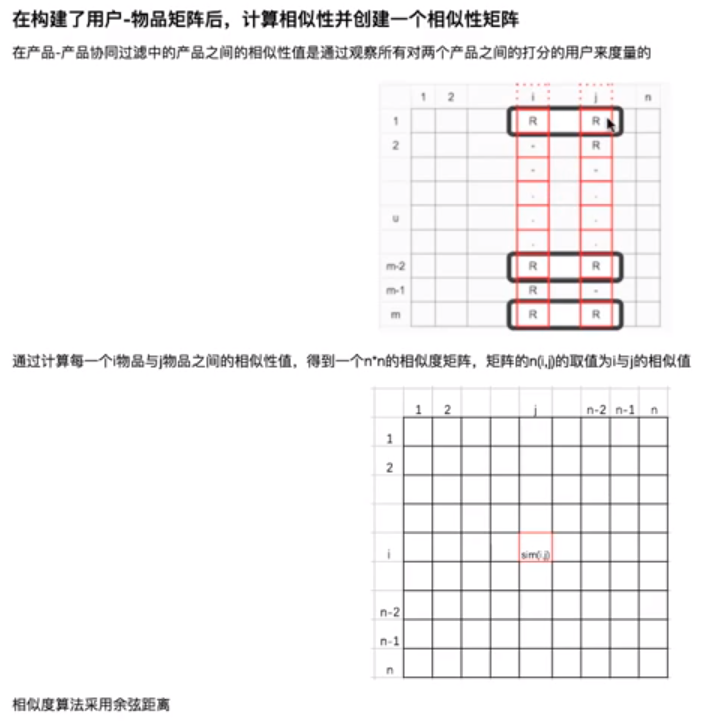
4.2 基于item的协同过滤推荐 - 预测原理

 

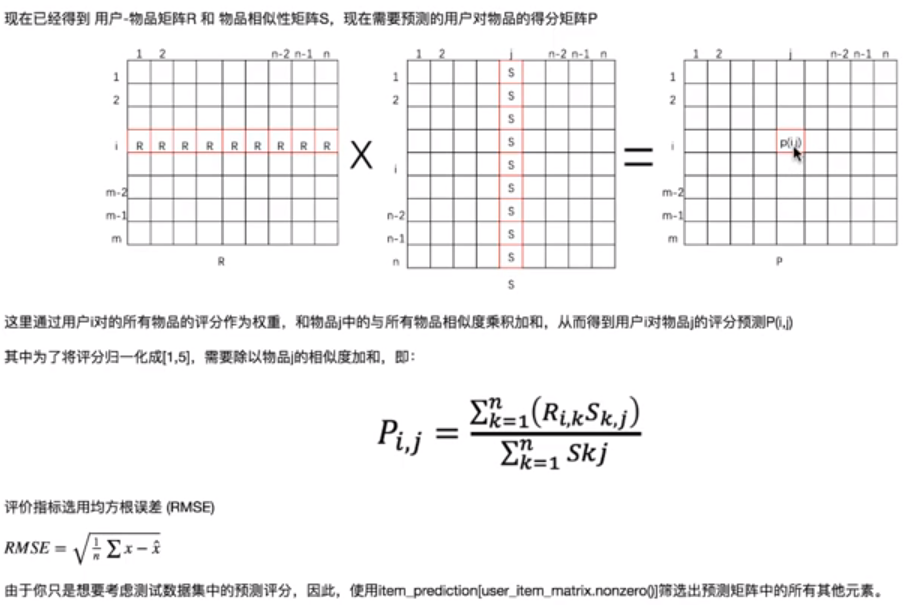
4.3 代码实现

 

1. import numpy as np
2. import pandas as pd
3. # 导入数据
4. data=pd.read_csv('ml-100k/u.data',sep='\t',names=['user_id','item_id','rating','timestamp'])
5. # 用户物品统计
6. n_users = data.user_id.nunique()
7. n_items = data.item_id.nunique()
8. # 拆分数据集
9. from sklearn.model_selection import train_test_split
11. train_data,test_data =train_test_split(data,test_size=0.3) #按照训练集70%，测试集30%的比例对数据进行拆分
13. # 训练集 用户-物品 矩阵
14. user_item_matrix = np.zeros((n_users,n_items))
15. for line in train_data.itertuples():
16. user_item_matrix[line[1]-1,line[2]-1] = line[3]
18. # 构建物品相似矩阵 - 使用sklearn.metrics.pairwise中的cosine计算余弦距离
19. '''
20. 采用余弦距离计算相似度
21. 如果两个物品在同一条水平线上，则其夹角为零，对应的余弦值为1，代表完全相似
22. 如果两个物品处于垂直的方向上，其夹角为90度，那么其余弦值为0，代表毫不相干
23. '''
24. from sklearn.metrics.pairwise import pairwise_distances
25. # 相似度计算定义为余弦距离
26. item_similarity_m = pairwise_distances(user_item_matrix.T,metric='cosine')
28. # 物品相似矩阵探索
29. '''
30. item_similarity_m.shape >> (1682, 1682)
32. item_similarity_m[0:5,0:5].round(2) # 取5*5的矩阵查看其保留两位小数的数据
33. # pairwise_distances模块在计算物品相似性时，不会计算自己与自己的相似性，所以所以对角线的值都为0
34. >> array([[0. , 0.67, 0.73, 0.7 , 0.81],
35. [0.67, 0. , 0.84, 0.64, 0.82],
36. [0.73, 0.84, 0. , 0.8 , 0.85],
37. [0.7 , 0.64, 0.8 , 0. , 0.76],
38. [0.81, 0.82, 0.85, 0.76, 0. ]])
39. '''
40. # 现在我们只分析上三角，得到等分位数
41. item_similarity_m_triu = np.triu(item_similarity_m,k=1) # 取得上三角数据
42. item_sim_nonzero = np.round(item_similarity_m_triu[item_similarity_m_triu.nonzero()],3)
43. '''
44. # 上三角矩阵
45. arr=np.linspace(1,9,9).reshape(3,3)
46. arr
47. >> array([[1., 2., 3.],
48. [4., 5., 6.],
49. [7., 8., 9.]])
50. np.triu(arr,k=1) # 默认k=0，k的值正数表示向右上角移对应个单位，把对应位置全部变为0
51. >> array([[0., 2., 3.],
52. [0., 0., 6.],
53. [0., 0., 0.]])
54. '''
55. # 查看十分位数
56. np.percentile(item_sim_nonzero,np.arange(0,101,10))

>> array([0. , 0.829, 0.884, 0.919, 0.948, 0.976, 1., 1.,1. , 1. , 1. ])

可以看出相似性得分普遍偏大，相似度没有比较好的可区分性。

 

4.4 训练集预测

 

1. user_item_precdiction = user_item_matrix.dot(item_similarity_m) / np.array([np.abs(item_similarity_m).sum(axis=1)])
2. # 除以np.array([np.abs(item_similarity_m).sum(axis=1)]是为了可以使评分在1~5之间，使1~5的标准化
4. # 只取数据集中有评分的数据集进行评估
5. from sklearn.metrics import mean_squared_error
6. from math import sqrt
7. prediction_flatten = user_item_precdiction[train_item_matrix.nonzero()]
8. user_item_matrix_flatten = train_item_matrix[train_item_matrix.nonzero()]
9. error_train = sqrt(mean_squared_error(prediction_flatten,user_item_matrix_flatten)) # 均方根误差计算
10. print('训练集预测均方根误差：'，error_train)

>> 训练集预测均方根误差：3.4714925320107684

 

4.5 测试集预测

 

1. test_data_matrix = np.zeros((n_users,n_items))
2. for line in test_data.itertuples():
3. test_data_matrix[line[1]-1,line[2]-1]=line[3]
5. # 预测矩阵
6. item_prediction = test_data_matrix.dot(item_similarity_m) / np.array(np.abs(item_similarity_m).sum(axis=1))
8. # 只取数据集中有评分的数据集进行评估
9. prediction_flatten = user_item_precdiction[test_data_matrix.nonzero()]
10. test_data_matrix_flatten = test_data_matrix[test_data_matrix.nonzero()]
11. error_test = sqrt(mean_squared_error(prediction_flatten,test_data_matrix_flatten)) # 均方根误差计算
12. print('测试集预测均方根误差：'，error_test)

>> 测试集预测均方根误差：3.4645810277607487

 

4.6 单模型结果提示思路

 

4.6.1 改变相似度算法 - 采用欧式距离

 

1. # 相似度计算定义为欧式距离
2. item_similarity_m = pairwise_distances(user_item_matrix.T,metric='euclidean')

>> 训练集预测均方根误差：3.3818902386408056
>> 测试集预测均方根误差：3.3763275676001396

 

4.6.2 增加训练集比例

 

1. from sklearn.model_selection import train_test_split
2. train_data,test_data =train_test_split(data,test_size=0.2)

>> 训练集预测均方根误差：3.4464124130045506
>> 测试集预测均方根误差：3.4247175440782516

 

4.6.3 增加训练集的同时采用欧式距离

>> 训练集预测均方根误差：3.3395618010919823
>> 测试集预测均方根误差：3.339569787071282

 

4.7 基于item协同过滤推荐系统结果分析

• 1、通过改变物品矩阵相似度（采用欧式距离）的计算方法可以看出预测效果略有提升；
• 2、通过增加训练集的方法对预测结果略有提升，但并不明显；
• 3、在增加训练集的同时采用欧式距离计算相似度发现预测效果提升最好，但均方根误差依然很大，与之前预测（物品是分位数查看结果，其区分性并不是很好）相符；
• 4、因而在此例中使用基于item的协同过滤推荐系统并不理想。

 

5 基于user的协同过滤的推荐系统

 

5.1 用户相似矩阵

 

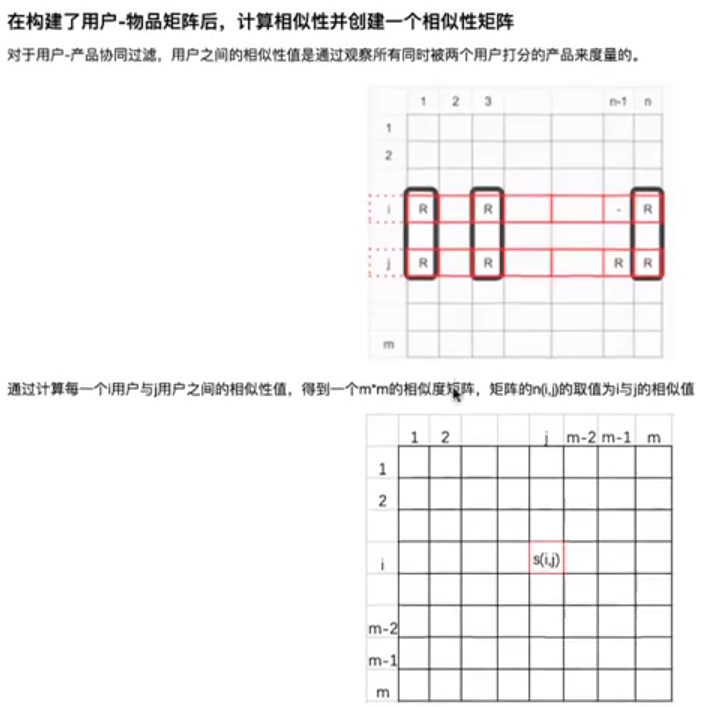
5.2 基于user的协同过滤的推荐系统 - 预测原理

 

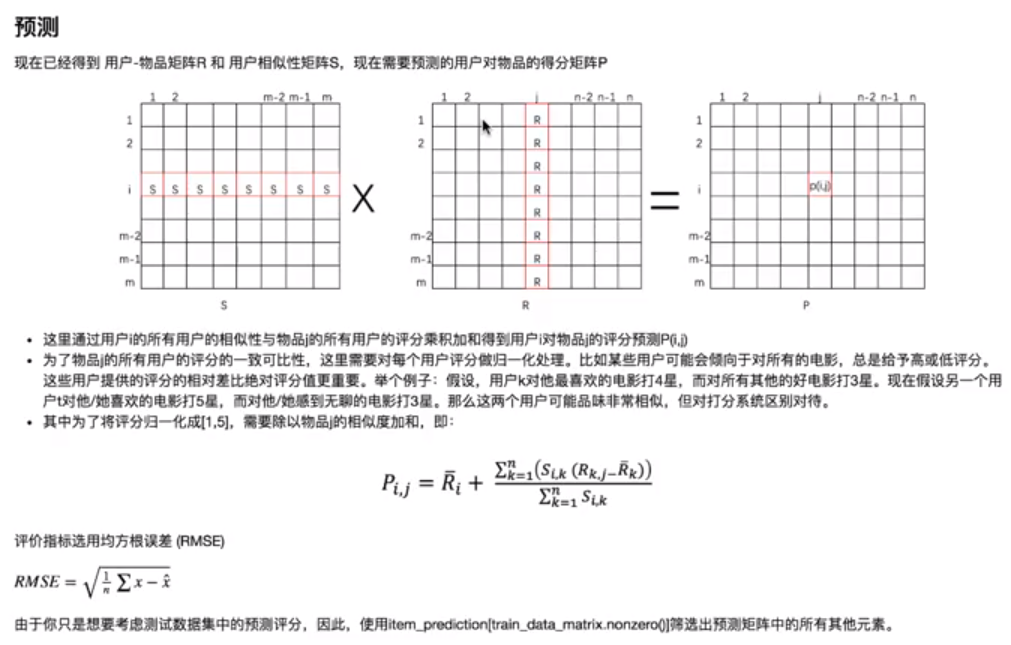
5.3 代码实现

 

1. # 导入数据
2. import numpy as np
3. import pandas as pd
4. data=pd.read_csv('ml-100k/u.data',sep='\t',names=['user_id','item_id','rating','timestamp'])
5. # 用户物品统计
6. n_users = data.user_id.nunique()
7. n_items = data.item_id.nunique()
8. # 拆分数据集
9. from sklearn.model_selection import train_test_split
10. # 按照训练集70%，测试集30%的比例对数据进行拆分
11. train_data,test_data =train_test_split(data,test_size=0.3)
12. # 训练集 用户-物品 矩阵
13. user_item_matrix = np.zeros((n_users,n_items))
14. for line in train_data.itertuples():
15. user_item_matrix[line[1]-1,line[2]-1] = line[3]
16. # 构建用户相似矩阵 - 采用余弦距离
17. from sklearn.metrics.pairwise import pairwise_distances
18. # 相似度计算定义为余弦距离
19. user_similarity_m = pairwise_distances(user_item_matrix,metric='cosine') # 每个用户数据为一行，此处不需要再进行转置
20. user_similarity_m[0:5,0:5].round(2) # 取5*5的矩阵查看其保留两位小数的数据
21. '''
22. >> array([[0. , 0.85, 0.96, 0.96, 0.74],
23. [0.85, 0. , 0.99, 0.84, 0.93],
24. [0.96, 0.99, 0. , 0.77, 0.97],
25. [0.96, 0.84, 0.77, 0. , 0.97],
26. [0.74, 0.93, 0.97, 0.97, 0. ]])
27. '''
28. # 现在我们只分析上三角，得到等分位数
29. user_similarity_m_triu = np.triu(user_similarity_m,k=1) # 取得上三角数据
30. user_sim_nonzero = np.round(user_similarity_m_triu[user_similarity_m_triu.nonzero()],3)
31. np.percentile(user_sim_nonzero,np.arange(0,101,10))

>> array([0.266,0.752,0.804,0.842,0.871,0.896,0.919,0.941,0.962,0.991, 1. ])

可以看出用户矩阵的相似性区分性还是比较好的

 

5.4 训练集预测

 

1. mean_user_rating = user_item_matrix.mean(axis=1)
2. rating_diff = (user_item_matrix - mean_user_rating[:,np.newaxis]) # np.newaxis作用：为mean_user_rating增加一个维度，实现加减操作
3. user_precdiction = mean_user_rating[:,np.newaxis] + user_similarity_m.dot(rating_diff) / np.array([np.abs(user_similarity_m).sum(axis=1)]).T
4. # 处以np.array([np.abs(item_similarity_m).sum(axis=1)]是为了可以使评分在1~5之间，使1~5的标准化
5. # 只取数据集中有评分的数据集进行评估
6. from sklearn.metrics import mean_squared_error
7. from math import sqrt
8. prediction_flatten = user_precdiction[user_item_matrix.nonzero()]
9. user_item_matrix_flatten = user_item_matrix[user_item_matrix.nonzero()]
10. error_train = sqrt(mean_squared_error(prediction_flatten,user_item_matrix_flatten)) # 均方根误差计算
11. print('训练集预测均方根误差：'，error_train)

>> 训练集预测均方根误差：3.165938175006113

 

5.5 测试集预测

 

1. test_data_matrix = np.zeros((n_users,n_items))
2. for line in test_data.itertuples():
3. test_data_matrix[line[1]-1,line[2]-1]=line[3]
5. # 预测矩阵
6. rating_diff = (test_data_matrix - mean_user_rating[:,np.newaxis]) # np.newaxis作用：为mean_user_rating增加一个维度，实现加减操作
7. user_precdiction = mean_user_rating[:,np.newaxis] + user_similarity_m.dot(rating_diff) / np.array([np.abs(user_similarity_m).sum(axis=1)]).T
10. # 只取数据集中有评分的数据集进行评估
11. prediction_flatten = user_precdiction[user_item_matrix.nonzero()]
12. user_item_matrix_flatten = user_item_matrix[user_item_matrix.nonzero()]
13. error_test = sqrt(mean_squared_error(prediction_flatten,user_item_matrix_flatten)) # 均方根误差计算
14. print('测试集预测均方根误差：'，error_test)

>> 测试集预测均方根误差：3.393103348518984

 

5.6 单模型结果提示思路

 

5.6.1 改变相似度算法 - 采用欧式距离

 

1. # 相似度计算定义为欧式距离
2. item_similarity_m = pairwise_distances(user_item_matrix.T,metric='euclidean')

>> 训练集预测均方根误差：3.1190848133071603
>> 测试集预测均方根误差：3.3913121798056123

 

5.6.2 减少训练集比例 / 增加测试集比例

 

1. from sklearn.model_selection import train_test_split
2. train_data,test_data =train_test_split(data,test_size=0.4)

>> 训练集预测均方根误差：3.237884760612846
>> 测试集预测均方根误差：3.34890617988761

 

5.6.2 增加训练集比例

 

1. from sklearn.model_selection import train_test_split
2. train_data,test_data =train_test_split(data,test_size=0.2)

>> 训练集预测均方根误差：3.094954182470391
>> 测试集预测均方根误差：3.435958471375406

 

5.6.3 增加测试集的同时采用欧式距离

>> 训练集预测均方根误差：3.1925775976328934
>> 测试集预测均方根误差：3.330738557937318

 

5.7 基于user协同过滤推荐系统结果分析

• 1、采用欧式距离的情况下，训练集数据预测效果提升较测试集明显；
• 2、运行结果显示基于user的预测结果在测试集上普遍不如在训练集上的预测结果。分析其原因：a.user相似矩阵本身太小（943*943），远小于item相似矩阵的（1682*1682）；b.在原因a的基础上，测试集的矩阵就更小；
• 2、因而基于user协同过滤系统中，分别采用了减小/增大训练集两种优化方法对模型进行了测试，发现只要数据集增大，其预测效果就有提升；
• 3、在减小训练集并采用欧式距离的情况下，模型在测试集的预测效果有所提升，但依然不理想；
• 4、与基于item的协同过滤系统相比，基于user协同过滤系统模型预测效果明显略微优秀。

 

6 基于SVD协同过滤推荐系统

 

6.1 SVD协同推荐系统原理

 

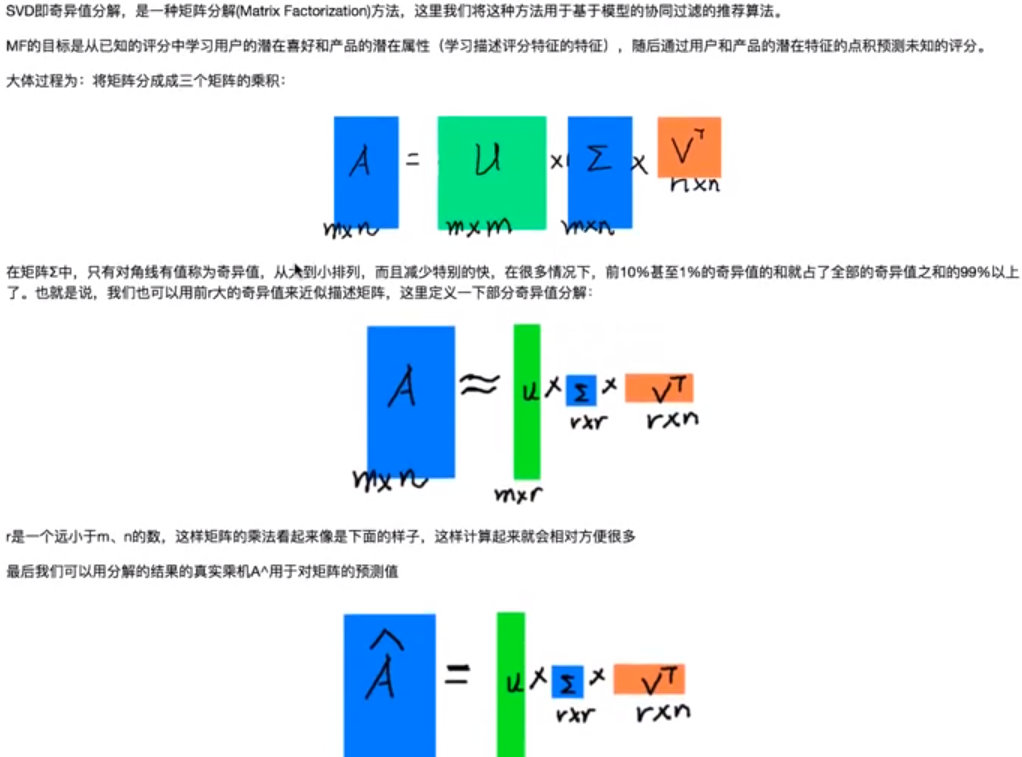
6.2 代码实现

 

1. # 导入数据
2. import numpy as np
3. import pandas as pd
4. data=pd.read_csv('ml-100k/u.data',sep='\t',names=['user_id','item_id','rating','timestamp'])
6. # 拆分数据集并分别构建用户-物品矩阵
7. # 用户物品统计
8. n_users = data.user_id.nunique()
9. n_items = data.item_id.nunique()
10. from sklearn.model_selection import train_test_split
11. # 按照训练集70%，测试集30%的比例对数据进行拆分
12. train_data,test_data =train_test_split(data,test_size=0.3)
13. # 训练集 用户-物品 矩阵
14. train_data_matrix = np.zeros((n_users,n_items))
15. for line in train_data.itertuples():
16. train_data_matrix[line[1]-1,line[2]-1] = line[3]
17. # 测试集 用户-物品 矩阵
18. test_data_matrix = np.zeros((n_users,n_items))
19. for line in train_data.itertuples():
20. test_data_matrix[line[1]-1,line[2]-1] = line[3]
22. # SVD矩阵
23. import scipy.sparse as sp
24. from scipy.sparse.linalg import svds
26. # 奇异值分解，超参数k的值就是设定要留下的特征值的数量
27. u, s, vt = svds(train_data_matrix,k=20)
28. s_diag_matrix = np.diag(s)
29. svd_prediction = np.dot(np.dot(u,s_diag_matrix),vt)
30. '''
31. print(u.shape) >> (943, 20)
32. print(s.shape) >> (20,)
33. print(vt.shape) >> (20, 1682)
34. print(s_diag_matrix.shape) >> (20, 20)
35. print(svd_prediction.shape) >> (943, 1682)
36. '''
37. # 预测值限定最小值和最大值
38. # 预测值小于0的均设置为0，大于5的均设置为5
39. svd_prediction[svd_prediction < 0] =0
40. svd_prediction[svd_prediction > 5] =5

 

6.3 训练集预测

 

1. # 只取预测数据中有评分的数据，进行评估
2. from sklearn.metrics import mean_squared_error
3. from math import sqrt
4. prediction_flatten = svd_prediction[train_data_matrix.nonzero()]
5. train_data_matrix_flatten = train_data_matrix[train_data_matrix.nonzero()]
6. error_train = sqrt(mean_squared_error(prediction_flatten,train_data_matrix_flatten))
7. print('训练集预测均方根误差：'，error_train)

>> 训练集预测均方根误差：2.440629842312816

 

6.4 测试集预测

 

1. prediction_flatten = svd_prediction[test_data_matrix.nonzero()]
2. test_data_matrix_flatten = test_data_matrix[test_data_matrix.nonzero()]
3. error_test = sqrt(mean_squared_error(prediction_flatten,test_data_matrix_flatten))
4. print('测试集预测均方根误差：'，error_test)

>> 测试集预测均方根误差：2.440629842312816

 

7 三大协同过滤推荐系统总结分析

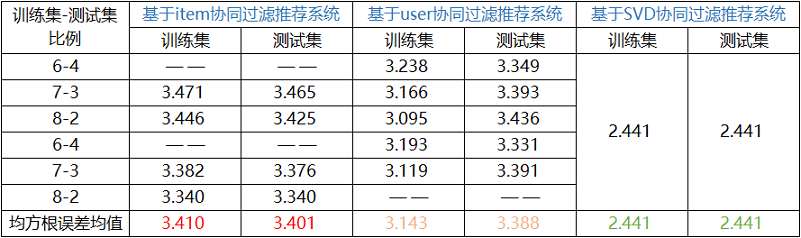
• 1、总体而言，基于小规模MovieLens数据集的本案例中的三大协同过滤推荐系统，其预测的效果总体上可以表示为：推荐系统预测效果：SVD > user > item。
• 2、根据基于user系统过滤推荐系统的情况可以看出，协同过滤推荐系统的数据越多，且数据之间互动越多，则推荐效果越好，然而一般情况下正是因为互动不够充分才会需要推荐系统，所以，收集尽可能多的数据，基于大数据的分析就显的相对比较重要；
• 3 在三大推荐系统中，SCD奇异值推荐系统表现尤为突出，预测的结果相对于其他两个推荐系统而言有非常大的提升，唯一的缺点就是其难以加以解释，但不失为是一种非常好的推荐系统。

 

NMF

参考

https://blog.csdn.net/qq_26225295/article/details/51165858

 

标签：matrix,SVD,NMF,item,算法,user,test,data,id
来源： https://www.cnblogs.com/lqerio/p/11193471.html