编程语言
首页 > 编程语言> > R语言高维数据的pca、 t-SNE算法降维与可视化分析案例报告

R语言高维数据的pca、 t-SNE算法降维与可视化分析案例报告

作者：互联网

维度降低有两个主要用例：数据探索和机器学习。它对于数据探索很有用，因为维数减少到几个维度（例如2或3维）允许可视化样本。然后可以使用这种可视化来从数据获得见解（例如，检测聚类并识别异常值）。对于机器学习，降维是有用的，因为在拟合过程中使用较少的特征时，模型通常会更好地概括。

在这篇文章中，我们将研究三维降维技术：

这些方法之间的关键区别在于PCA输出旋转矩阵，可以应用于任何其他矩阵以转换数据。另一方面，诸如t分布随机邻居嵌入（t-SNE）的基于邻域的技术不能用于此目的。

加载威士忌数据集

  我们可以通过以下方式加载数据集：

 
df <- read.csv(textConnection(f), header=T)
# select characterics of the whiskeys
features <- c("Body", "Sweetness", "Smoky",
            "Medicinal", "Tobacco", "Honey",
            "Spicy", "Winey", "Nutty",
            "Malty", "Fruity", "Floral")
feat.df <- df[, c("Distillery", features)]

关于结果的假设

在我们开始减少数据的维度之前，我们应该考虑数据。我们期望具有相似味道特征的威士忌在缩小的空间中彼此接近。

由于来自邻近酿酒厂的威士忌使用类似的蒸馏技术和资源，他们的威士忌也有相似之处。
为了验证这一假设，我们将测试来自不同地区的酿酒厂之间威士忌特征的平均表达是否不同。为此，我们将进行MANOVA测试：

##           Df Pillai approx F num Df den Df    Pr(>F)    
## Region     5 1.2582   2.0455     60    365 3.352e-05 ***
## Residuals 80                                            
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

检验统计量在5％水平上是显着的，因此我们可以拒绝零假设（区域对特征没有影响）。这意味着适当的降维应该在一定程度上保持酿酒厂的地理位置。

酿酒厂的地理位置

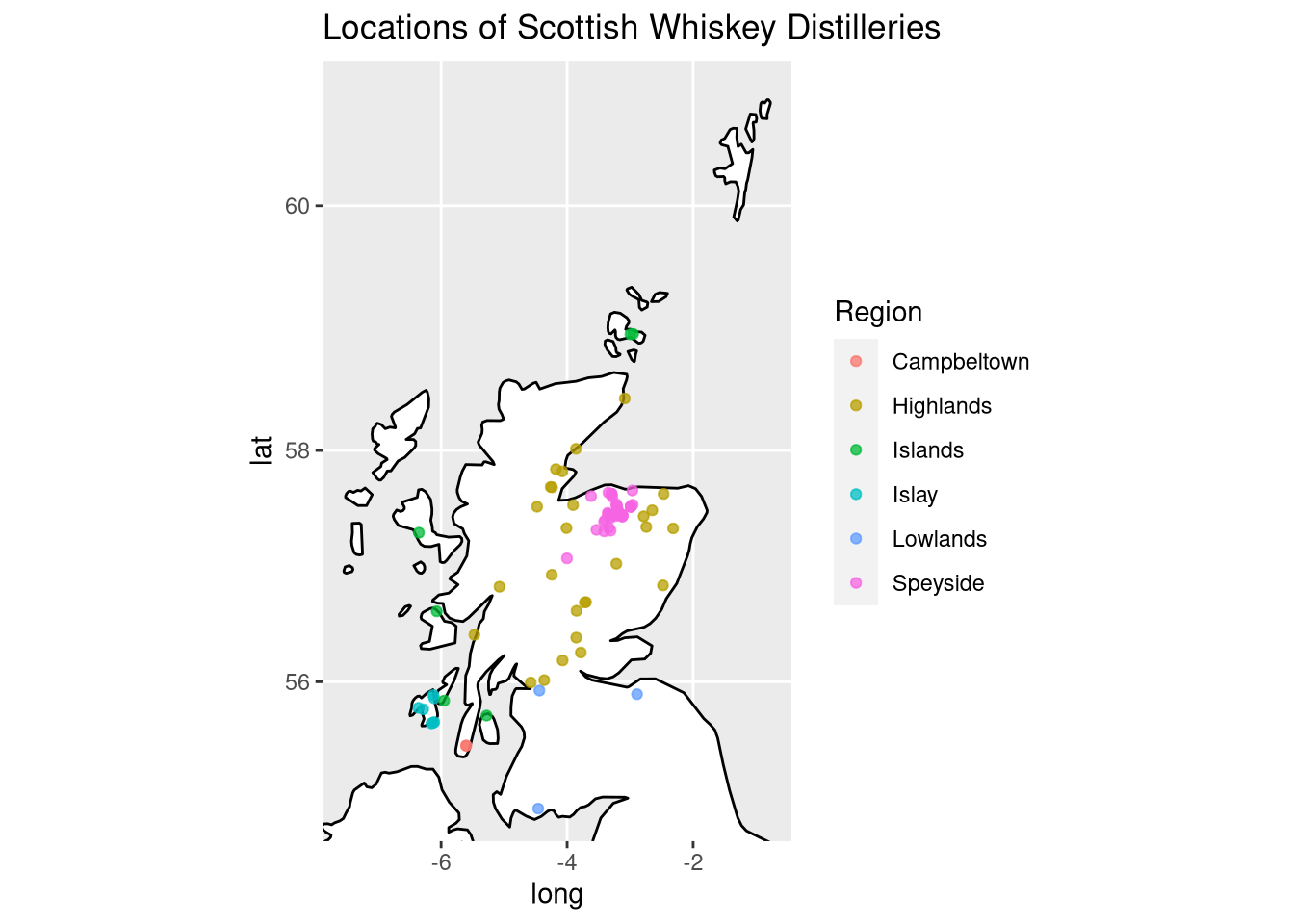
由于区域性对威士忌起着重要作用，我们将通过绘制其纬度和经度来探索数据集中的酿酒厂所在的位置。以下苏格兰威士忌地区存在：

苏格兰地区（根据CC BY-SA 3.0许可，并从https://commons.wikimedia.org/wiki/File:Scotch_regions.svg检索）​

苏格兰地区（根据CC BY-SA 3.0许可，并从https://commons.wikimedia.org/wiki/File:Scotch_regions.svg检索）

 

​

 

 

PCA

使用PCA可视化威士忌数据集

PCA通常使用该prcomp功能执行。在这里，我们使用，autoplot因为我们主要对可视化感兴趣。

 

​

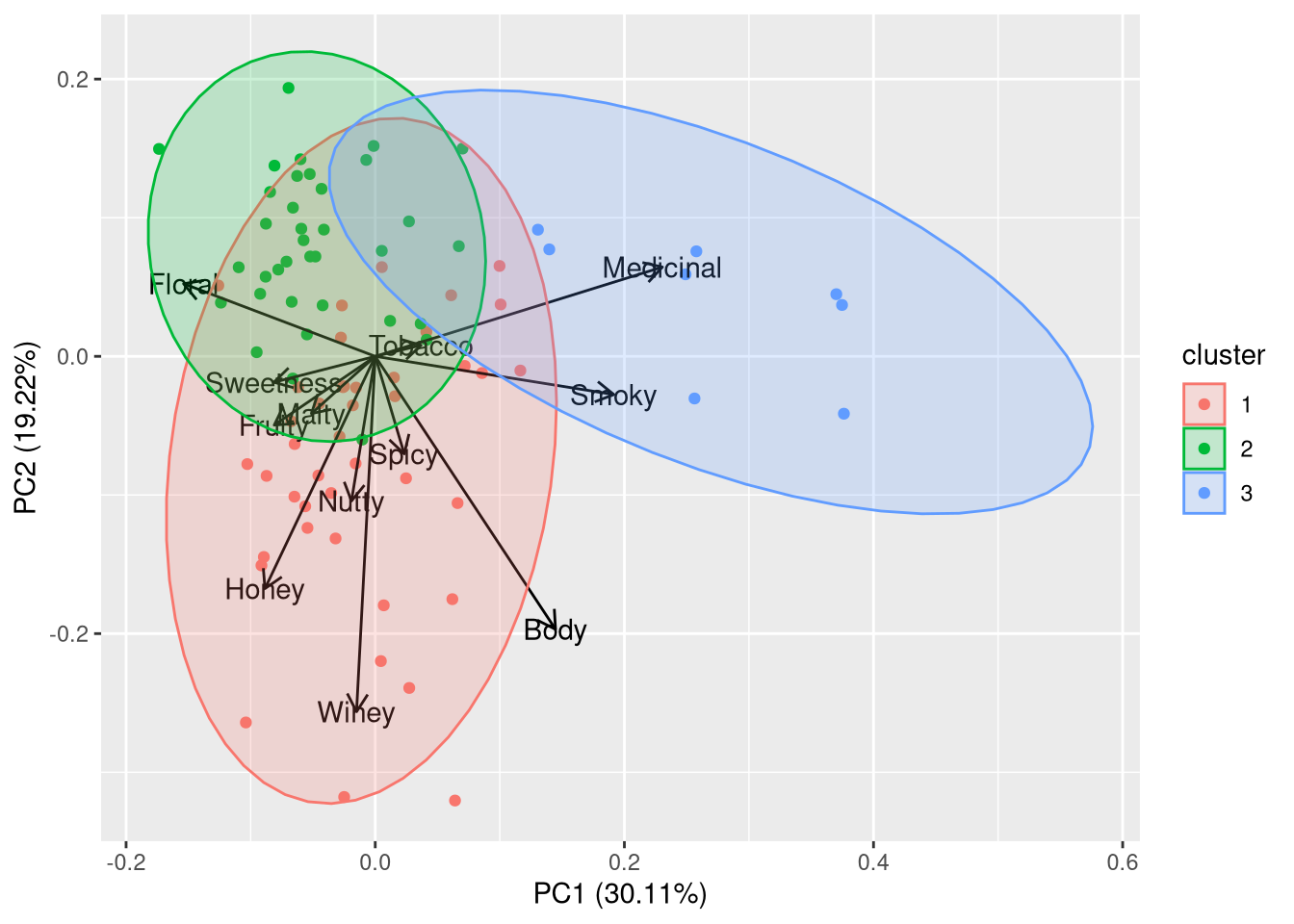
在第二个图中，我们将绘制酿酒厂的标签，以便我们可以更详细地解释聚类。

​

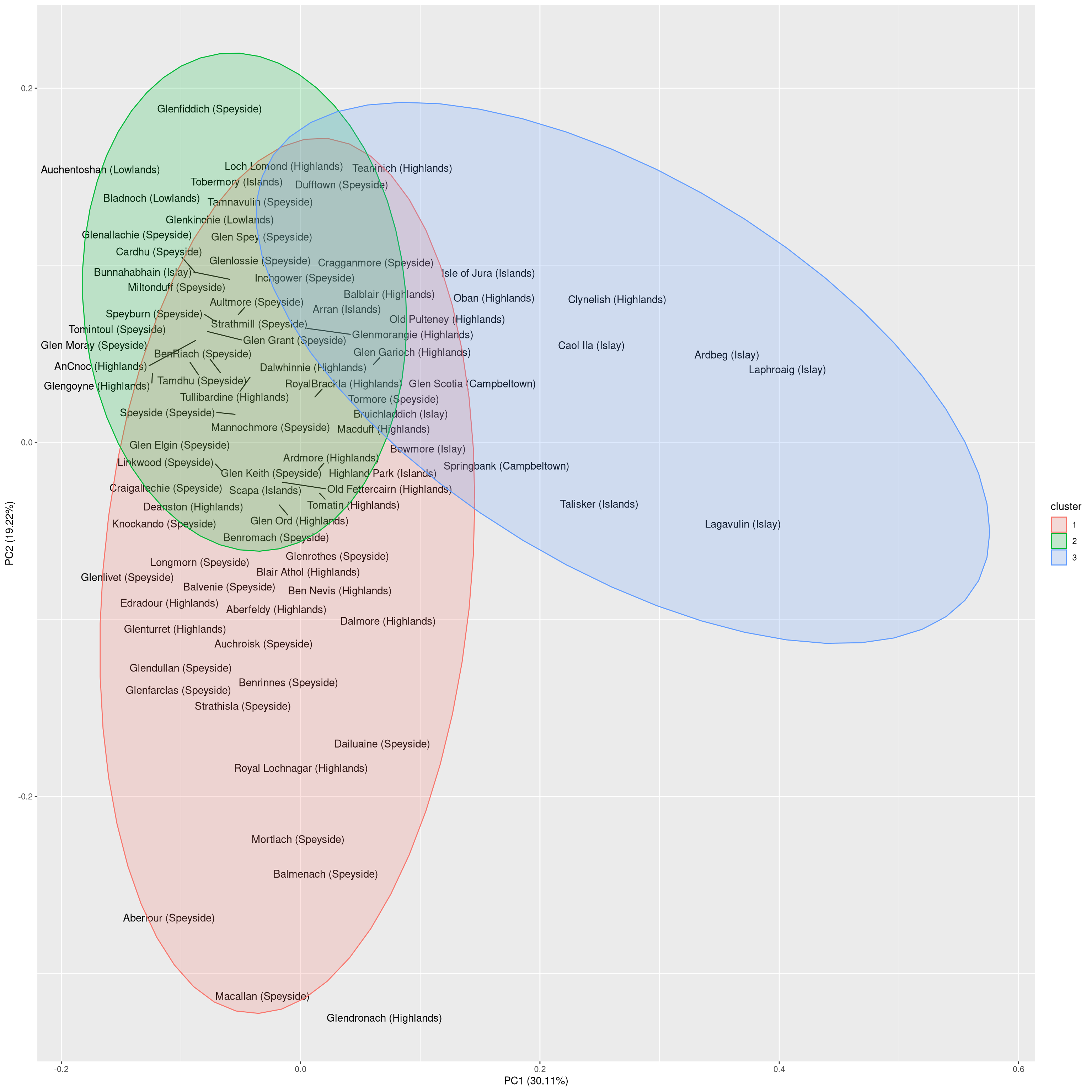
总的来说，主要成分似乎反映了以下特征：

让我们验证群集是否实际上过多地代表了某些区域：

##   Cluster Campbeltown Highlands Islands Islay Lowlands Speyside
## 1       1           2        17       2     2        0       19
## 2       2           0         8       2     1        3       22
## 3       3           0         2       2     4        0        0

实际上，每个集群都展示了一个过多的区域。对集群的合理解释如下：

可视化有两个有趣的观察结果：

这包含了我们对PCA的可视化研究。我们将在本文末尾研究使用PCA进行预测。

核PCA

内核PCA（KPCA）是PCA的扩展，它利用了内核函数，这些函数在支持向量机上是众所周知的。通过将数据映射到再现内核Hilbert空间，即使它们不是线性可分的，也可以分离数据。

 

在R中使用KPCA

要执行KPCA，我们使用包中的kpca函数kernlab。

 

其中σσ是反向内核宽度。使用此内核，可以按如下方式减少维数：

​

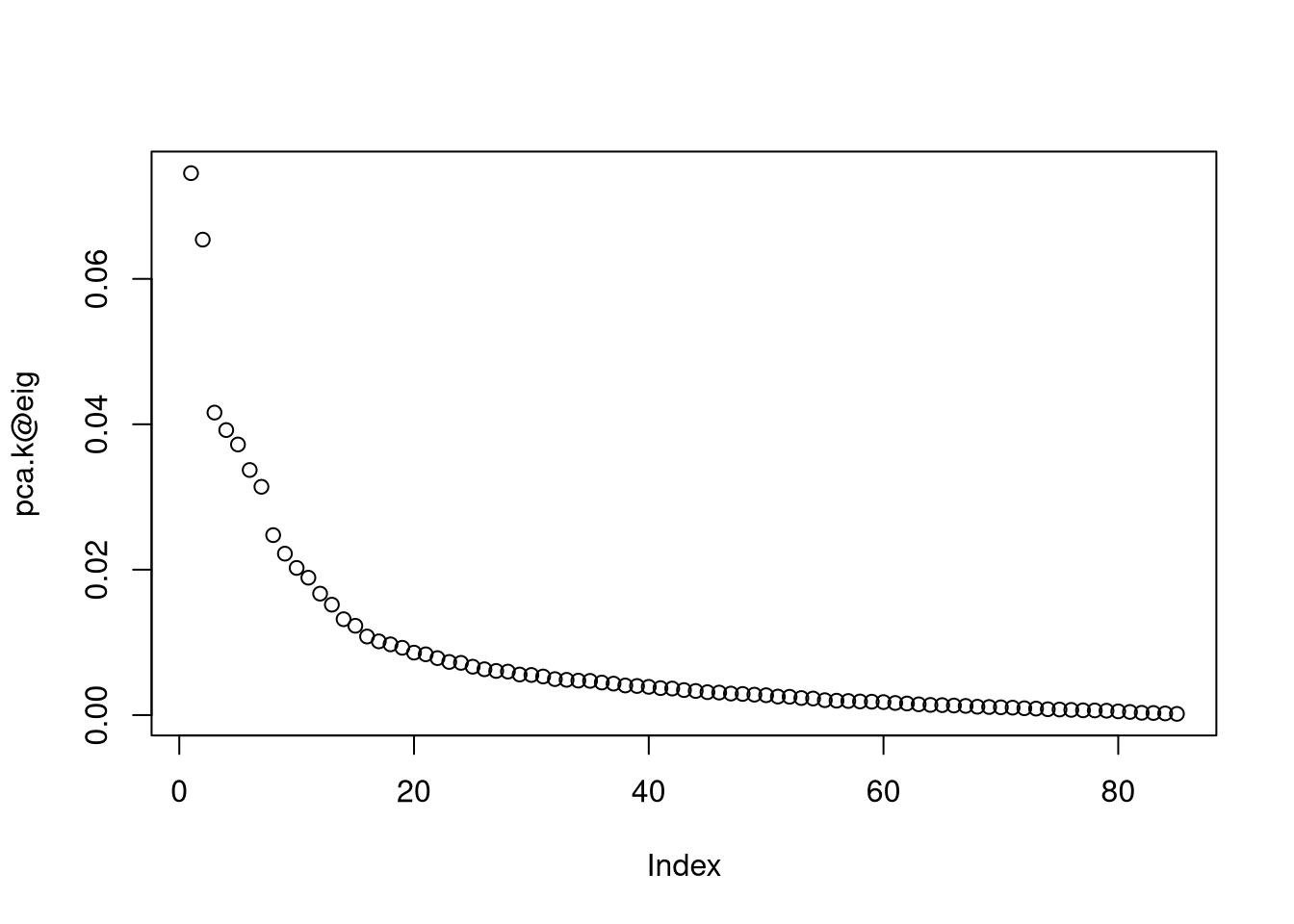
检索到新维度后，我们现在可以在转换后的空间中可视化数据：

​

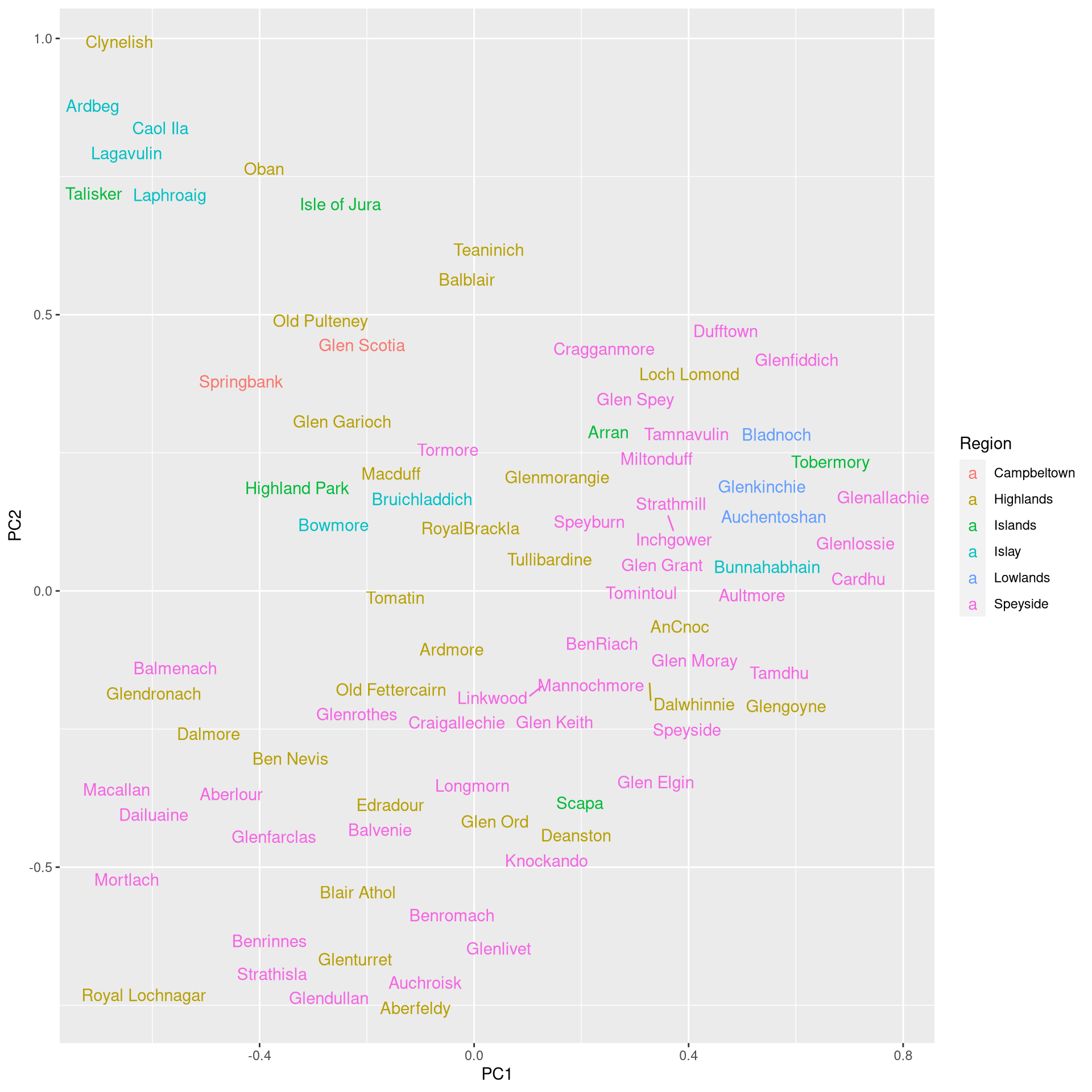
就可视化而言，结果比我们使用常规PCR获得的结果稍微粗糙一些。尽管如此，来自艾莱岛的威士忌分离得很好，我们可以看到一群斯佩塞特威士忌，而高地威士忌则高度传播。

KPCA的一个缺点是你需要处理内核函数的超参数：这些需要调整到数据。此外，KPCA不像PCA那样可解释，因为无法确定各个维度解释了多少方差。

T-SNE

t-SNE于2008年推出。从那时起，它已成为一种非常流行的数据可视化方法。t-SNE执行两个算法步骤。首先，构建对样本对的概率分布PP该分布将高选择概率分配给相似对，将低概率分配给不相似对。

 

在t-SNE中，困惑平衡了数据的局部和全局方面。它可以解释为与每个点关联的近邻的数量。建议的困惑范围是5到50.由于t-SNE是概率性的并且还具有困惑度参数，因此它是一种非常灵活的方法。但是，这可能使人对结果有点怀疑。请注意，t-SNE不适用于监督学习等设置，因为生成的维度缺乏可解释性。

使用t-SNE可视化数据

使用R，t-SNE可以通过Rtsne从包中加载具有相同名称的函数来执行。在这里，我们将威士忌数据集的维度降低到两个维度：

​

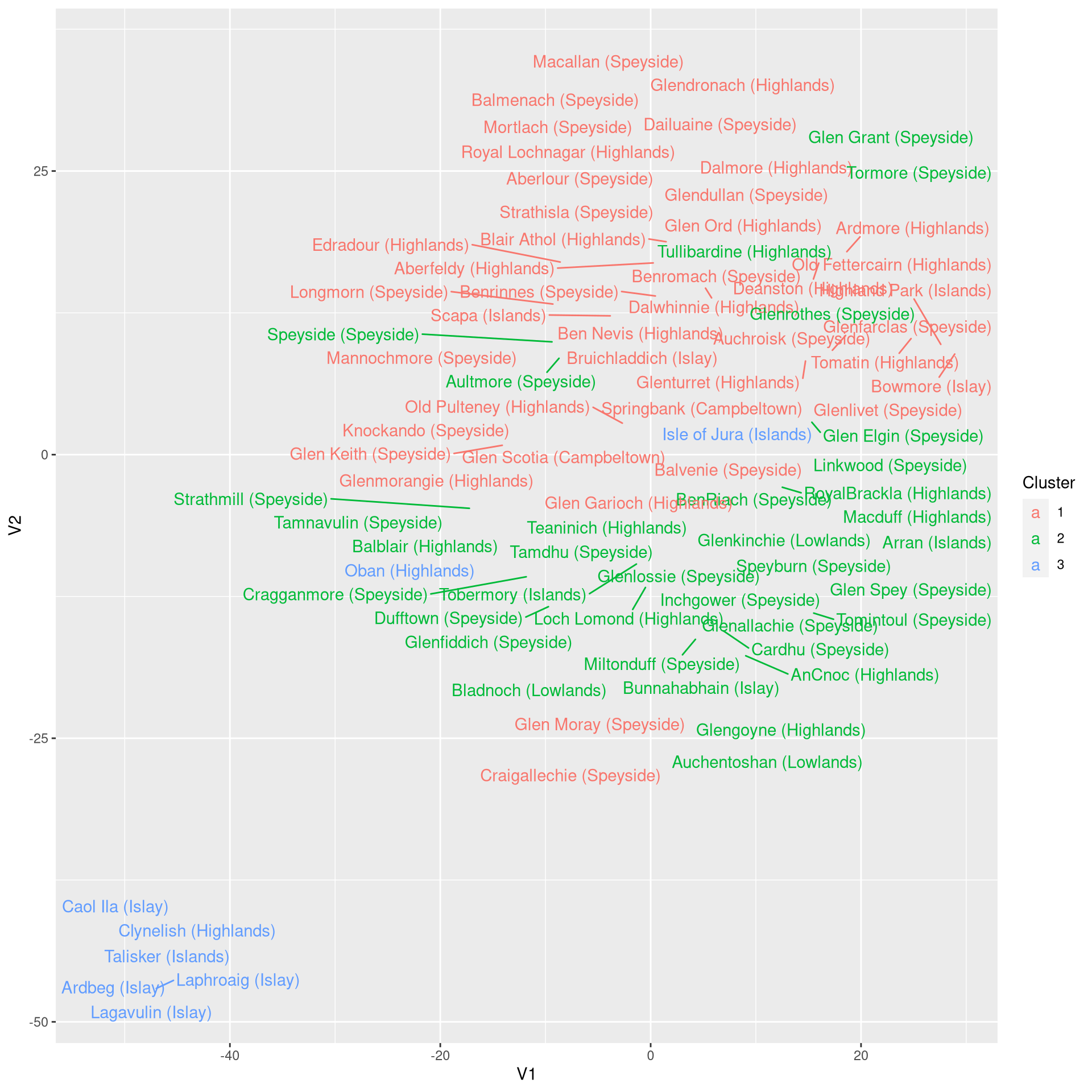
用t-SNE获得的维数降低的结果令人印象深刻。与PCA相比，簇的分离更加清晰，特别是对于簇1和簇2。

然而，解释对于t-SNE来说有点单调乏味。使用PCA，我们利用负载来获得有关主要组件的见解。对于t-SNE尺寸，我们必须手动进行解释：

使用PCA进行监督学习

对于培训和测试数据集，PCA是独立完成的，这一点至关重要。为什么？如果对整个数据集执行PCA，则通过PCA获得的正交投影将受到测试数据的影响。因此，当在测试数据上测试模型的性能时，模型的性能将被高估，因为投影被调谐到测试样本所在的空间。因此，需要遵循以下方法：

  1. 在测试数据集上执行PCA并在转换后的数据上训练模型。
  2. 将训练数据中的学习PCA变换应用于测试数据集，并评估模型在变换数据上的性能。

为了举例说明工作流程，让我们根据其口味特征预测威士忌的起源区域。为此，我们将使用ķk最近邻模型，因为我们拥有的少数特征（p = 12）将通过PCA进一步减少。此外，因为所有的变量是在特征空间小[0,4][0,4]。由于我们必须优化kk，因此我们还预留了用于确定此参数的验证集。

PCA转换

首先，我们编写一些函数来验证预测的性能。我们将简单地使用此处的准确度，尽管另一个性能指标可能更合适，因为很少有样本可用的区域可能会更频繁地混淆。此外，我们将50％的观察值分配给训练集，25％分配给验证集（用于调整kk），25％分配给测试集（用于报告性能）。

get.accuracy <- <strong>function</strong>(preds, labels) {
    correct.idx <- which(preds == labels)
    accuracy <- length(correct.idx) / length(labels)
    <strong>return</strong>(accuracy)
}
select.k <- <strong>function</strong>(K, training.data, test.data, labels, test.labels) {
    <span style="color:#888888"># report best performing value of k</span>
    performance <- vector(<span style="color:#880000">"list"</span>, length(K))
    <strong>for</strong> (i <strong>in</strong> seq_along(K)) {
        k <- K[i]
        preds <- knn(train = training.data, test = test.data, 
                     cl = labels, k = k)
        validation.df <- cbind(<span style="color:#880000">"Pred"</span> = as.character(preds), <span style="color:#880000">"Ref"</span> = as.character(test.labels))
        <span style="color:#888888">#print(k)</span>
        <span style="color:#888888">#print(validation.df)</span>
        accuracy <- get.accuracy(preds, test.labels)
        performance[[i]] <- accuracy
    }
    <span style="color:#888888"># select best performing k</span>
    k.sel <- K[which.max(performance)]
    <strong>return</strong>(k.sel)
}
set.seed(<span style="color:#880000">1234</span>) <span style="color:#888888"># reproducibility</span>
samp.train <- sample(nrow(data), nrow(data)*<span style="color:#880000">0.50</span>) <span style="color:#888888"># 50 % for training</span>
df.train <- data[samp.train,,]
<span style="color:#888888"># 25% for validation</span>
samp.test <- sample(setdiff(seq(nrow(data)), samp.train), length(setdiff(seq(nrow(data)), samp.train)) * <span style="color:#880000">0.5</span>)
df.test <- data[samp.test,]
samp.val <- setdiff(seq_len(nrow(data)), c(samp.train, samp.test))
df.val <- data[samp.val, ]</code></span></span>

在下面的代码中，我们将对训练数据执行PCA并研究解释的方差以选择合适的维数

##         [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## N_dim      1    2    3    4    5    6    7    8    9    10    11    12
## Cum_Var   22   41   52   63   72   79   85   90   94    97    99   100

由于有足够百分比的方差用3维解释，我们将使用该值来设置训练，测试和验证数据集。这里，我们使用该predict.princomp函数将从训练数据获得的旋转矩阵应用到其他数据集。请注意，此函数的名称具有误导性，因为它并不能真正预测任何内容。

现在我们已经将训练，验证和测试集转换为PCA空间，我们可以使用kk最近邻居。请注意，这种预测方案具有挑战性，因为岛屿和低地等一些地区的代表性不足。如果我们将选择kk具有非常大的值（例如K = 30），则最样本将被分配到过多的区域。由于我们使用精度作为性能度量，因此这样的分类器实际上可能表现良好。因此，我们保守地限制kk的范围以避免选择这样的模型。

## [1] "PCA+KNN accuracy for k = 9 is: 0.571"

让我们研究一下使用PCA的模型是否优于基于原始数据的模型：

## [1] "KNN accuracy for k = 7 is: 0.524"

kkTobaccoMalty

<span style="color:#000000"><span style="color:#000000"><code><span style="color:#888888"># variances of whiskeys characteristics</span>
print(diag(var(data)))</code></span></span>
##      Body Sweetness     Smoky Medicinal   Tobacco     Honey     Spicy 
## 0.8656635 0.5145007 0.7458276 0.9801642 0.1039672 0.7279070 0.6157319 
##     Winey     Nutty     Malty    Fruity    Floral 
## 0.8700410 0.6752394 0.3957592 0.6075239 0.7310534

现在我们只能根据他们的口味确定苏格兰威士忌的六个区域，但问题是我们是否仍能获得更好的表现。我们知道很难预测数据集中代表性不足的苏格兰地区。那么，如果我们将自己局限于更少的地区，会发生什么？PCA分析表明我们可以通过以下方式重新组合标签：

通过这种方式，问题减少到三个区域：Island / Islay威士忌，Highland / Lowland / Campbeltown威士忌和Speyside威士忌。让我们再次进行分析：

## [1] "PCA+KNN accuracy for k = 13 is: 0.619"

我们可以得出61.9％的准确度，我们可以得出结论，将我们样品较少的威士忌区域分组确实是值得的。

KPCA用于监督学习

应用KPCA进行预测并不像应用PCA那样简单。在PCA中，特征向量是在输入空间中计算的，但在KPCA中，特征向量来自核心希尔伯特空间。因此，当我们不知道所使用的显式映射函数ϕϕ，不可能简单地转换新数据点。

很容易就是根据转换后的数据创建模型。但是，这种方法对验证没有帮助，因为这意味着我们将测试集包含在PCA中。因此，以下方法中的方法不应用于验证模型：

<span style="color:#000000"><span style="color:#000000"><code><strong>library</strong>(class) <span style="color:#888888"># for knn</span>
Z <- pca.k@rotated[,<span style="color:#880000">1</span>:(n.dim.model)] <span style="color:#888888"># the transformed input matrix</span>
preds.kpca <- knn(train = Z[samp.train,], test = Z[samp.test,], 
                     cl = df$Region[samp.train], k = k.sel.pca)
<span style="color:#888888"># NB: this would overestimate the actual performance</span>
accuracy <- get.accuracy(preds.kpca, df$Region[samp.test])</code></span></span>

除了这个属性，KPCA可能并不总是减少功能的数量。这是因为内核函数实际上导致参数数量的增加。因此，在某些情况下，可能无法找到尺寸小于最初的投影。

摘要

在这里，我们看到了如何使用PCA，KPCA和t-SNE来降低数据集的维数。PCA是一种适用于可视化和监督学习的线性方法。KPCA是一种非线性降维技术。t-SNE是一种更新的非线性方法，擅长可视化数据，但缺乏PCA的可解释性和稳健性。

 

我觉得有趣的是威士忌的二维投影包含大的开放区域。这可能表明以下两点之一：

  1. 尝试新的，令人兴奋的威士忌仍有很大的潜力。
  2. 有很多种味道的组合是可能的，并且很好地结合在一起。

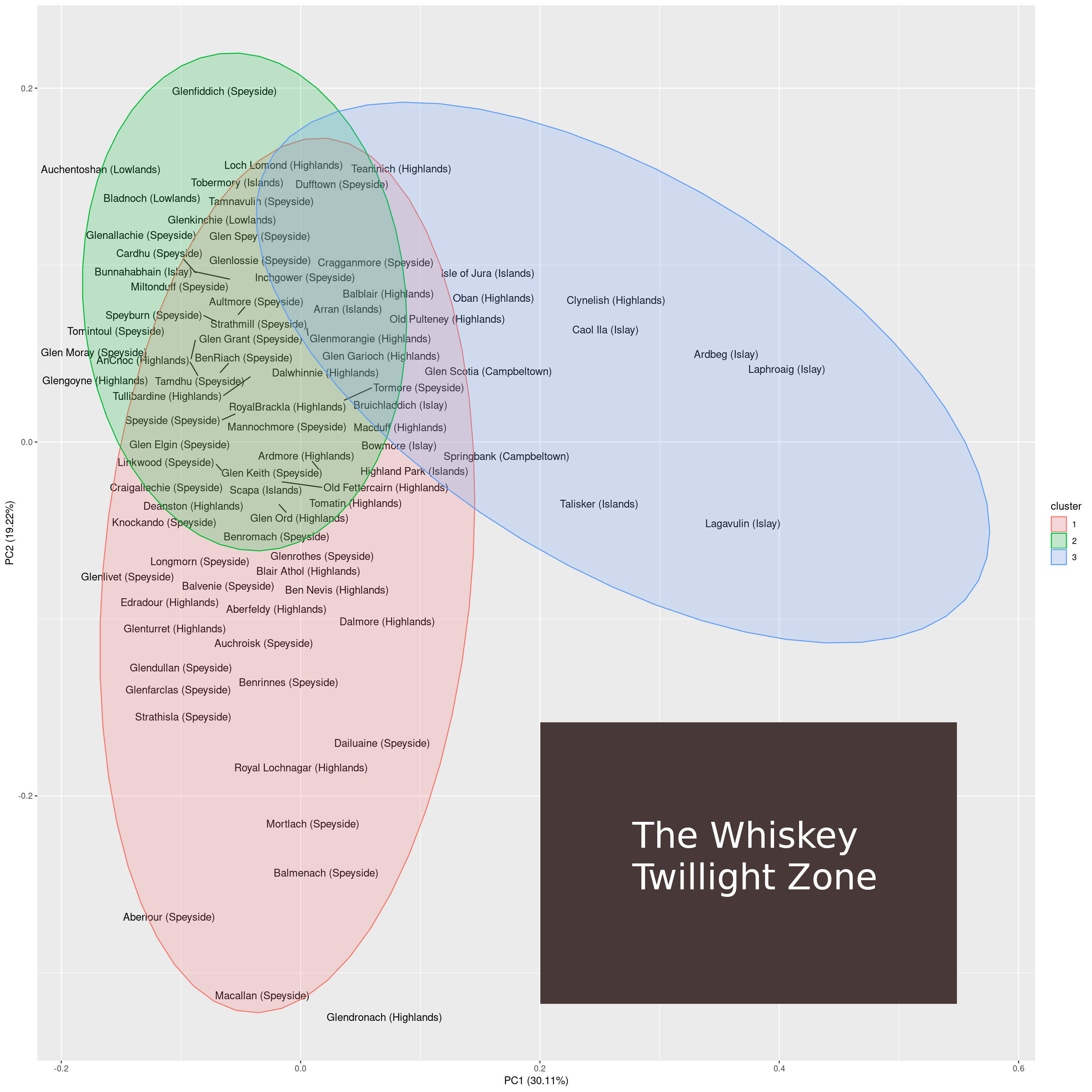
我倾向于选择第二种选择。为什么？在PCA图中，右下角是没有样本所在的最大区域。看着靠近这个区域的威士忌，我们发现那些是y轴上的Macallan和x轴上的Lagavulin。麦卡伦以其复杂的口味而闻名，Lagavulin以其烟熏味而闻名。

位于二维PCA空间右下方的威士忌将同时具有两种特性：它既复杂又烟熏。我猜这种具有两种特性的威士忌对于口感来说太过分了（即烟熏掩盖了复杂性）。

这个未开发的味道区域可以被认为是威士忌暮光区域。关于暮光区，有两个问题。首先，是否可以生产威士忌来填补空白，其次，可能更重要的是，这些威士忌的味道如何？

威士忌暮光之城​

 

有问题吗？联系我们！

 

大数据部落 -中国专业的第三方数据服务提供商，提供定制化的一站式数据挖掘和统计分析咨询服务

统计分析和数据挖掘咨询服务：y0.cn/teradat（咨询服务请联系官网客服）

点击这里给我发消息​QQ：3025393450

​

【服务场景】  

科研项目; 公司项目外包;线上线下一对一培训;数据采集;学术研究;报告撰写;市场调查。

【大数据部落】提供定制化的一站式数据挖掘和统计分析咨询服务

【大数据部落】大数据部落提供定制化的一站式数据挖掘和统计分析咨询服务​

标签：SNE,##,降维,PCA,威士忌,pca,数据,我们
来源： https://www.cnblogs.com/tecdat/p/10913673.html