编程语言
首页 > 编程语言> > CSP-J考试复习：第二单元 基础算法 2.7 ​​​​​​​2的k次方进制数

CSP-J考试复习：第二单元 基础算法 2.7 ​​​​​​​2的k次方进制数

作者：互联网

2.7 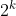2^{k}进制数

【问 题描述】
设 r   是个 2
k 进制 数（  1≤k≤9），并满足以下条件：
(1)  r 至 少 是 个 2 位的 2
k进制数。 
(2)  作为 2 
 k  进制数， 除 最后一位外，r 的每一位严格小于它右边相邻的一位。

   (3 ) 将 r 转  换为 2 进制数 q 后，则 q 的总位数不超过 w（k＜w≤30000）。
 输入  k  和  W，请满足上述条件的不同 r 的数量。
【  分析】 
 本   题不可能直接 枚举——答案不超过 200 位，说明用到了高精度算法！
先不 考虑  w。 对于一个 m 位数来讲，m 个数字的顺序是确定的。所以只需直接从 n（n ＝2
k－1） 个数中 取
m  个数 ， 组 成 m 位数。所以符合条件的 m 位数有Cm
n个。   
现 在考虑 w 存在的情况。这里有一个明显的事实：2
 k 进制数 ，除 首位外，每一位转化为二进制后都是 k 个
二  进制位 。 现在最大的问题就是 2
k  进制数的首位 。
二进 制不超过 w  位的数，在 2
 k 进制 下就是 a ＝[w/k]＋1 位（w 能被 k 整除时，认为首位有 0 个数字）。此
时首位 剩下 b＝w%  k 个二进制位，即最大可以取 2
b－1。接 下来 只需针对 2
k进制下位数不足 a  和恰好为 a 两种
情况分别 进 行枚举。 
所以，符 合条 件 的 2 
                                                                                                                                                              k进制数个数 为  f\left ( k,w \right )=\left\{\begin{matrix} \sum_{i=2}^{n}C_{n}^{i} &w\geq k \\ \sum_{i=2}^{a-1}C_{n}^{i}+\sum_{i=1}^{2^{b}-1}C_{n-i}^{a}&k< w< kn \end{matrix}\right.

其中   n = 2^{k}-1,a=\left [ w/k \right ]+1,b=w      mod  k                                                                                                                                                                                                                      
通 过排列组合，我们间接地枚举了所有符合条件的解。  

标签：进制,个数,首位,枚举,位数,次方,2.7,CSP
来源： https://blog.csdn.net/zhengheda/article/details/120373563